


Examen
mai 2002
On désire mettre en mémoire deux images f et g dont les valeurs sont entières et comprises respectivement dans les intervalles [0, 255] et [0, 1]. On s'intéresse à la manière de représenter ces images en mémoire.
Citez plusieurs moyens de représenter f et g.
Comparez les représentations (efficacité, taille mémoire, etc) dans le cas des images f et g.
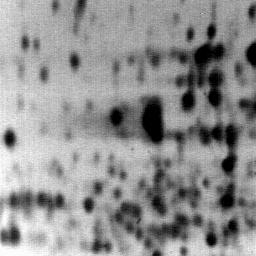
Soient trois images et la norme de la transformée de FOURIER de l'une d'entre elles.
 |
 |
 |
||
| (a) | (b) | (c) | ||

|
||||
| (d) (en vidéo inverse!) | ||||
A quelle image (a, b ou c) correspond la norme de la transformée de
FOURIER telle que montrée en (d), en vidéo inverse? Argumentez
votre réponse.
Soit la fonction f suivante
| 19 | 25 | 33 | 35 | 36 | 23 | 44 | 69 |
| 100 | 19 | 25 | 33 | 35 | 36 | 23 | 44 |
| 100 | 50 | 19 | 25 | 33 | 35 | 36 | 23 |
Calculez les filtres de SOBEL de cette image f.
Pour la suite de la question, on considère la fonction unidimensionnelle suivante:
| 19 | 25 | 33 | 35 | 36 | 23 | 44 | 69 |
Que vaut l'image reconstruite après érosion par un segment centré, large de 3 points?
On désire réaliser le contrôle industriel d'un tuyau servant au transport du pétrole. Pour cela, on réalise l'imagerie d'une coupe transversale 2D de ce tuyau par un procédé de tomographie par rayons X en géométrie parallel-beam. Le schéma géométrique du tuyau est le suivant:
La densité du matériau constituant le barreau vaut 1, 0 tandis que les densités intérieure et extérieure sont nulles.
Déterminez la transformée de RADON de la fonction 2D f (x, y) caractérisant cette tranche. Esquissez une des projections obtenues.
Montrez que le théorème du profil central de la transformée de FOURIER est vérifié.
Montrez sans calcul que si le tuyau ne présente aucun défaut, une seule projection permet la reconstruction exacte de f (x, y).
Suggestions:
On désire traiter l'image suivante

Proposez une méthode pour extraire la totalité du grillage. Expliquez également comment vous traitez les bords.
Démontrer ou donner un contre-exemple:
Une image et cette même image tournée de 1800 ont la même transformé de FOURIER en amplitude.
Pour toute fonction f
|
(f |
(1) |
Pour toute fonction f et tout segment linéaire horizontal H
|
R(f |
(2) |