Examen
mai 2001
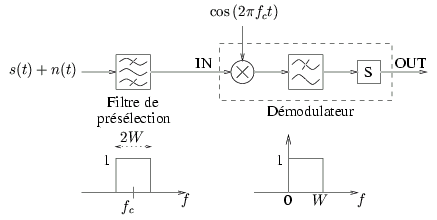
On désire étudier les performances d'un démodulateur AM vis à vis du bruit. Considérons le schéma de démodulation suivant:

Étant donné le signal modulant m(t), le signal modulé est donné par
Le signal reçu, composé du signal modulé et d'un bruit blanc additif
gaussien n(t) de densité spectrale de puissance N0/2,
est tout d'abord filtré par un filtre passe-bande de bande
![]() fc - W, fc + W
fc - W, fc + W![]() .
Après pré-filtrage, le signal passe au travers d'un démodulateur synchrone
composé d'un mélangeur, d'un filtre passe-bas et d'un suppresseur
S de composante continue idéal.
.
Après pré-filtrage, le signal passe au travers d'un démodulateur synchrone
composé d'un mélangeur, d'un filtre passe-bas et d'un suppresseur
S de composante continue idéal.
On définit le rapport signal à bruit (noté SNR) en un point d'un système comme le rapport entre la puissance moyenne du signal utile et la puissance du bruit en ce point:
Quel est le rôle du premier filtre?
Calculez le rapport signal sur bruit (SNR)IN à l'entrée du démodulateur.
Calculez le rapport signal sur bruit (SNR)OUT à la sortie du démodulateur.
Un récepteur est caractérisé par sa figure de mérite définie par
Un important théorème de SHANNON précise qu'il est possible, dans le cas d'un canal additif gaussien, de calculer la capacité C d'un canal exprimée en [b/s] telle que, pour tout débit binaire fb inférieur à C, la probabilité d'erreur sur bits tende vers 0. Cette capacité vaut
Exprimez la capacité d'un canal dans le cas d'un récepteur NRZ pour
un débit de 1 [kb/s] et un rapport
![]() = 35 [dB].
= 35 [dB].
Que vaut le rapport
![]() (en [dB]) lorsque
B
(en [dB]) lorsque
B ![]()
![]() ?
?
Citez les noms des 4 couches inférieures du modèle OSI.
Formulaire spécifique:
| log2x | = | ||
| ln(1 + x) | = | x - |
Considérez une modulation en bande de base du type PAM à 4 niveaux de tension. Le schéma du démodulateur utilisé est le suivant
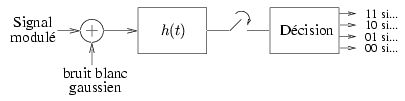
où le filtre h(t) est adapté à l'impulsion de mise en forme
![]() (t) de durée T et d'amplitude unitaire.
(t) de durée T et d'amplitude unitaire.
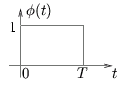
Un bruit blanc gaussien de densité spectrale de puissance égale à N0/2 est présent à l'entrée du filtre adapté. Le détail de la modulation PAM-4 utilisée est donné dans le tableau suivant
| Symbole | Probabilité d'émission | Mise en forme |
| 00 | 0,25 |
- |
| 01 | 0,25 |
- V |
| 10 | 0,25 |
+ V |
| 11 | 0,25 |
+ |
et le débit de transmission est égal à (2/T) bits/secondes.
Dans un premier temps, on considère ![]() = 2.
= 2.
Dessinez la sortie du filtre adapté pour la séquence d'entrée 011101010011. Différenciez les deux cas où le filtre est implémenté par convolution et par intégration.
Étant donné que le symbole 10 a été transmis, déterminez la probabilité de commettre une erreur de décision. Exprimez cette probabilité d'erreur en fonction de T, N0 et V.
Que vaut la probabilité calculée en (2) lorsque
![]() = 10?
= 10?
Commentez le choix des valeurs des amplitudes des symboles (avec ![]() = 2).
= 2).
Pour rappel,
Dans une transmission radio numérique, on désire assurer une couverture dans un rayon de 50 [km] autour de l'antenne émettrice. Le niveau du champ électrique minimum requis pour avoir une réception de qualité a été fixé à 2 [mV/m]. L'antenne émettrice présente une aire effective de 1,4 [m2] et la fréquence de l'onde porteuse est égale à 100 [MHz].
Déterminez la Puissance Isotrope Rayonnée Équivalente (PIRE) nécessaire pour assurer la couverture voulue.
Calculez la gain de l'antenne d'émission.
Sachant que l'on se donne une marge de 3 [dB] afin de palier aux problèmes de transmission liés aux intempéries fréquentes dans cette région, calculez la puissance de l'émetteur.
Calculez la puissance reçue par un récepteur situé à 30 km de l'émetteur et présentant un gain d'antenne de 2 [dB].