Principes des télécommunications analogiques et numériques

Examen
août 2001

Formulaire

Relations trigonométriques

$$\mp$$ (1)

sin(A±B) = sin A cos B±cos A sin B (2)

$${\textstyle\frac{1}{2}}$$ (3)

$${\textstyle\frac{1}{2}}$$ (4)

$${\textstyle\frac{1}{2}}$$ (5)

Transformées de FOURIER

$${\frac{t}{T}}$$ T sinc(fT) (6)

$${\frac{1}{2W}} {\frac{f}{2W}}$$ sinc(2Wt) (7)

$${\frac{1}{a+2\pi jf}}$$ e^-atu(t),  a > 0 (8)

$${\frac{2a}{a^{2}+(2\pi f)^{2}}}$$ e^{-a| t|},  a > 0 (9)

$$\pi \pi$$ (10)

$$\delta$$ 1 (11)

$$\delta$$ 1 (12)

$$\delta \pi$$ (13)

$$\pi \delta$$ (14)

$$\pi {\textstyle\frac{1}{2}} \delta \delta$$ (15)

$$\pi {\frac{1}{2j}} \delta \delta$$ (16)

$${\frac{1}{\pi jf}}$$ sgn(t) (17)

$${\frac{1}{\pi t}}$$ - jsgn(f ) (18)

$${\textstyle\frac{1}{2}} \delta {\frac{1}{2\pi jf}}$$ u(t) (19)

$$\sum_{i=-\infty }^{+\infty } \delta {\frac{1}{T_{0}}} \sum_{n=-\infty }^{+\infty } \delta {\frac{n}{T_{0}}}$$ (20)

Question 1

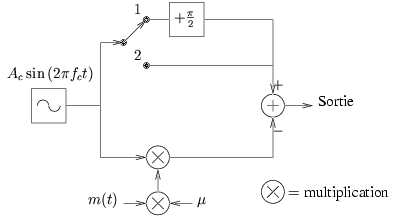
Considérez le circuit de la figure suivante:

où m(t) est un signal que l'on désire moduler et $\mu$ une constante.

1. En supposant que $\left\vert\vphantom{ \mu m(t)}\right.$$\mu$ m(t)$\left.\vphantom{ \mu m(t)}\right\vert$ $\ll$ 1, montrez que si l'interrupteur est en position 1, la sortie du circuit correspond à une modulation angulaire à bande étroite. S'agit-il d'une modulation de phase ou de fréquence?

2. Déterminez le spectre du signal modulé ainsi obtenu.

3. Si l'interrupteur est en position 2, quel type de signal obtient-on à la sortie du circuit ? Comparez son spectre à celui du signal précédent.

Question 2

Une antenne montée sur un satellite géostationnaire, alimentée par une puissance de 10 [W], émet à une fréquence de 13 [GHz] en direction d'une antenne terrestre avec laquelle elle est en parfait alignement. La station terrestre en question est équipée d'une antenne de 3 [m] de rayon, située à une distance de 40000 [km] et présentant un défaut d'alignement de 0, 2^o. La puissance reçue par la station terrestre est de 25 [pW]. L'affaiblissement dû au passage de l'onde électro-magnétique à travers l'atmosphère est égale à 0, 3 [dB]. L'efficacité $\eta$ de l'antenne terrestre est de 0,59 tandis que celle du satellite est de 0,55. Pour rappel,

L_alignement = 12$$\left(\vphantom{ \frac{\alpha Df}{70c}}\right.$$$${\frac{\alpha Df}{70c}}$$$$\left.\vphantom{ \frac{\alpha Df}{70c}}\right)^{2}_{}$$

où L_alignement est exprimé en [dB] et $\alpha$ en [^o].

1. Donnez l'expression de la puissance isotrope rayonnée équivalente en fonction des paramètres présents dans l'énoncé.

2. Donnez l'expression de la puissance reçue en fonction des paramètres présents dans l'énoncé.

3. Déterminez la valeur numérique de l'affaiblissement en espace libre. Exprimez-la en [dB].

4. Déterminez la valeur numérique du gain de l'antenne montée sur le satellite. Exprimez-la en [dB].

Question 3

En vue de sa transmission en bande de base, on désire échantillonner, quantifier et coder un signal m(t) dont la fonction d'autocorrélation est donnée par

$$\Gamma_{mm}^{}$$($$\tau$$) = $${\frac{3 (0.001)^{2}}{(0.001)^{2}+(2\pi \tau )^{2}}}$$

N'étant pas à bande limitée, on réalise un pré-filtrage du signal de telle sorte que le signal filtré conserve 90% de la puissance du signal de départ.

1. Quelle est la puissance en [W], [dBW] et [dBm] du signal m(t) avant filtrage ?

2. Déterminez la fréquence d'échantillonage minimum à utiliser.

3. Étant donné un rapport signal-bruit de quantification minimum de 30 [dB], déterminez le nombre de bits à attribuer par échantillon sachant que l'amplitude maximum du signal filtré est égale à 4 [V].

4. Le signal m(t) est échantillonné à la fréquence de 5 [kHz]. Déterminez le débit binaire de la transmission.

5. Si l'onde PCM obtenue est transmise en utilisant un codage de MANCHESTER, déterminez la bande passante minimum du canal de transmission.

Question 4

Pour transmettre une onde PCM binaire présentant un débit R_b = 1/T, on utilise une modulation en bande de base utilisant une impulsion de mise en forme $\phi$(t) en cosinus surélevé afin de limiter au maximum les interférences inter-symboles. Les caractéristiques de la modulation sont les suivantes:

Symbole	Représentation physique	Probabilité d'émission
1	+ $\phi$(t) [V]	2/3
0	- $\phi$(t) [V]	1/3

où $\phi$(t) est donnée par

$$\phi$$(t) = $$\left\{\vphantom{ \begin{array}{cc} \frac{1}{2}+\frac{1}{2}\cos \... ...) & \textrm{si }\vert t\vert\leq T/2\\ 0 & \textrm{sinon} \end{array}}\right.$$$$\begin{array}{cc} \frac{1}{2}+\frac{1}{2}\cos \left( \frac{2\pi t}{T}\right) & \textrm{si }\vert t\vert\leq T/2\\ 0 & \textrm{sinon} \end{array}$$

et représentée graphiquement par

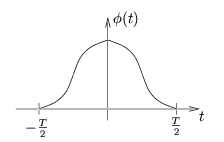
1. Déterminez la densité spectrale de puissance du signal modulé sachant que les symboles sont non-corrélés.

2. Déterminez la bande passante du signal modulé et comparez-la à celle de la modulation NRZ de la même onde PCM.

Remarque:

Pour rappel, la densité spectrale de puissance vaut

$$\gamma_{g }^{}$$(f )= $$\left\Vert\vphantom{ \Phi (f) }\right.$$$$\Phi$$(f )$$\left.\vphantom{ \Phi (f) }\right\Vert^{2}_{}$$$${\frac{1}{T}}$$$$\left[\vphantom{ \sigma _{A }^{2}+\mu _{A }^{2}\sum ^{+\infty }_{m=-\infty }\frac{1}{T}\delta (f-\frac{m}{T})}\right.$$$$\sigma_{A }^{2}$$ + $$\mu_{A }^{2}$$$$\sum^{+\infty }_{m=-\infty }$$$${\frac{1}{T}}$$$$\delta$$(f - $${\frac{m}{T}}$$)$$\left.\vphantom{ \sigma _{A }^{2}+\mu _{A }^{2}\sum ^{+\infty }_{m=-\infty }\frac{1}{T}\delta (f-\frac{m}{T})}\right]$$