Date: août 2002
On dispose d'un enregistrement
{x[0], x[1], ..., x[N - 1]}
de durée N d'un signal aléatoire X(t) stationnaire au sens large.
Soit l'estimateur de puissance suivant
Cet estimateur est-il biaisé?
Donnez l'expression analytique de la variance de cet estimateur.
L'évaluation de la variance de l'estimateur est-elle aisée? Commentez votre réponse.
Soit un radar embarqué sur un satellite et destiné à obtenir des images
précises du sol terrestre. Pour y parvenir, le radar envoie des impulsions
de courte durée ![]() avec une certaine fréquence de répétition.
Il mesure ensuite les impulsions reçues après réflexion sur la surface
terrestre. Comme le coefficient de réflexion sur la terre dépend des
propriétés électromagnétiques du sol, on peut reconstituer une image
de la surface.
avec une certaine fréquence de répétition.
Il mesure ensuite les impulsions reçues après réflexion sur la surface
terrestre. Comme le coefficient de réflexion sur la terre dépend des
propriétés électromagnétiques du sol, on peut reconstituer une image
de la surface.
Le schéma général se présente comme suit:
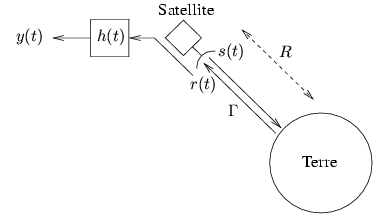
Enfin, les impulsions émises ont la forme
Que vaut la fréquence instantanée fi(t) du signal? (pour rappel,
fi(t) = ![]()
![]() où
où ![]() (t) représente
l'argument du cosinus)
(t) représente
l'argument du cosinus)
Dessinez l'allure de s(t). Quelle est sa particularité? Calculez ensuite son enveloppe complexe.
L'expression de l'enveloppe complexe du signal reçu est donnée par
Déterminez l'expression du signal r(t) reçu par le récepteur après
réflexion sur le sol terrestre, en fonction de s(t), ![]() et
et ![]() .
.
Le signal reçu r(t) est ensuite filtré par un filtre de réponse
fréquentielle
![]() (f ). En se basant sur les enveloppes complexes
du signal reçu y(t) et du signal émis s(t), déterminez les spectres
de
(f ). En se basant sur les enveloppes complexes
du signal reçu y(t) et du signal émis s(t), déterminez les spectres
de
![]() (f ) et de l'enveloppe complexe
E
(f ) et de l'enveloppe complexe
E![]() (f )
du filtre utilisé à la réception. On suppose que, si le gain en amplitude
du filtre est
(f )
du filtre utilisé à la réception. On suppose que, si le gain en amplitude
du filtre est ![]() ,
K
,
K![]()
![]() 1.
1.
Dessinez le module
![]()
![]() (f )
(f )![]() et la
phase
et la
phase ![]() (f ) de ce filtre. Quelle est sa particularité?
(f ) de ce filtre. Quelle est sa particularité?
Suggestions pour la partie (5):
Considérer la modulation 2-4PSK qui correspond exactement à une modulation
OQPSK sauf que la durée de l'impulsion rectangulaire de mise en forme
n'est plus égale à 2Tb mais bien à Tb. Autrement dit,
l'onde de mise en forme vaut + V pour
t ![]() [0, Tb] et 0
pour
t
[0, Tb] et 0
pour
t ![]() ]Tb, 2Tb].
]Tb, 2Tb].
Pour la séquence binaire 10110010110..., représentez les composantes en phase et en quadrature, l'enveloppe et la phase du signal modulé.
Représentez le plan de constellation (plan complexe de es(t)).
Que vaut la largeur de bande d'un signal modulé en OQPSK?
Comparez la largeur de bande d'une modulation 2-4PSK à celle d'une OQPSK.
Déterminez la densité spectrale de puissance du signal modulé si les symboles ont une probabilité d'émission donnée par
On considère le système de transmission à spectre étalé représenté par le schéma suivant:

où
Première partie: dans un premier temps, on cherche
à trouver l'expression analytique de la densité spectrale de bruit
à la sortie de l'intégrateur. Le signal de bruit vaut
n(t) = Ancos(2![]() fct +
fct + ![]() )
où
)
où ![]() est une phase aléatoire de moyenne nulle.
est une phase aléatoire de moyenne nulle.
Que vaut le facteur d'étalement?
Donnez l'expression analytique du signal v1(t) à l'entrée du récepteur.
Quel signal v2(t) trouve-t-on à l'entrée de l'intégrateur?
Si l'on prend
fc = ![]() , certains termes de v2(t)
auront une contribution nulle à la sortie de l'intégrateur. Quels
sont ces termes? (Indications: (1) pensez à développer les
cosinus, (2) les termes
cos
, certains termes de v2(t)
auront une contribution nulle à la sortie de l'intégrateur. Quels
sont ces termes? (Indications: (1) pensez à développer les
cosinus, (2) les termes
cos![]() et
sin
et
sin![]() ne dépendent
pas du temps et sont donc constants sur toute la période d'intégration)
ne dépendent
pas du temps et sont donc constants sur toute la période d'intégration)
Comme toutes les opérations sont linéaires, il est possible de négliger les termes de contribution nulle dès l'entrée l'intégrateur. Que vaut donc ce signal v3(t) simplifié, tiré de l'expression de v2(t)?
Que est le terme d'interférence contenu dans v3(t)?
Que vaut la densité spectrale du terme d'interférence à l'entrée de l'intégrateur?
Que vaut la densité spectrale du terme d'interférence à la sortie de l'intégrateur? Pour les calculs, on peut considérer que l'intégrateur agit comme un passe-bas idéal jusqu'à la fréquence fb.
Seconde partie: on désire calculer la probabilité
d'erreur sur bit Pe. Pour rappel, dans le cas d'une modulation
BPSK classique, la probabilité d'erreur sur bit Pe vaut
On supposera que la densité spectrale de bruit est constante pour
![]() f
f![]()
![]() fb et vaut
fb et vaut
Cette densité spectrale est nulle pour en dehors de l'intervalle
[- fb, fb].
![]() est une constante.
est une constante.
Calculez la valeur de Pe. (Indication: pensez à remplacer Eb par sa valeur)
Quel gain réalise-t-on par rapport à une BPSK classique si l'on considère
que ![]() est une variable aléatoire uniformément distribuée
sur l'intervalle [0, 2
est une variable aléatoire uniformément distribuée
sur l'intervalle [0, 2![]() ]?
]?
Le gain est-il dû à l'étalement?