La théorie de l'information cherche à établir l'information inhérente
à un processus probabiliste; elle part d'un principe qu'un événement
certain n'apporte aucune information, au contraire d'un événement
rare lorsque celui-ci survient. Considérons un événement aléatoire
E qui se produit avec une probabilité p(E).
Définition 18
L'information propre de l'événement E,
notée i(E) est le logarithme en base 2 de l'inverse de sa probabilité
i(E) = log2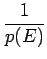 = - log2p(E) = - log2p(E) |
(2.10) |
Elle s'exprime en bit.
Si p(E) = 1, c'est-à-dire que l'événement E est certain, i(E) = 0
et l'information associée à E est donc nulle. Par contre, si p(E) = 0, 9,
le fait que E se réalise apporte une certaine quantité d'information.
Dès lors, plus un événement est incertain, plus on lui attribue de
l'information. À la limite, un événement de probabilité nulle a une
information propre infinie. Cependant, un événement qui ne se produit
jamais n'est pas très intéressant.
Marc Van Droogenbroeck. Tous droits réservés.
2004-06-15