| (8.7) |
Au moyen de cette notation, on écrit la forme matricielle d'un mot codé
| (8.7) |
La matrice G est appelée matrice génératrice. Elle a pour expression générale
G = 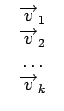  |
(8.8) |
Exemple. Dans le cas des signaux MPEG, la matrice
génératrice se ramène à
G = 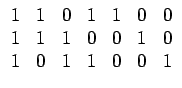 |
(8.9) |
| = | (110)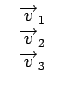 |
(8.10) | |
| = | (1101100) |
(8.11) | |
| = | (0011110) | (8.12) |
En prenant toutes les combinaisons possibles pour les éléments du message (il y en a 2k), on génère 2k vecteurs dispersés dans un espace à n dimensions. En d'autres termes, l'effet du code est de répartir 2k messages dans un espace comprenant 2n messages. Plus ces messages seront éloignés entre eux, plus la probabilité de les confondre diminuera et plus la résistance au bruit augmentera. C'est là tout l'enjeu des codes.