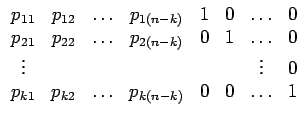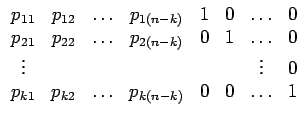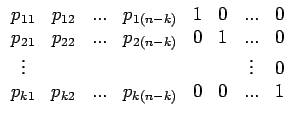Table des matières of 8.3.5 Code systématique

8.3.5 Code systématique

Définition 44 Un code est dit systématique si une partie du mot codé coïncide avec le message.

Dans le cas d'un code systématique, il est d'usage de placer le message original dans la seconde partie du mot codé. Dès lors, la matrice G s'exprime comme

G	=	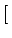$\displaystyle \left[\vphantom{P\,\vert\, I_{k}}\right.$ P \| I_k $\displaystyle \left.\vphantom{P\,\vert\, I_{k}}\right]$	(8.15)
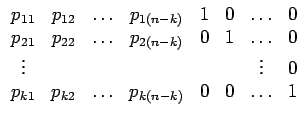	=	$\displaystyle \left[\vphantom{\begin{array}{cccccccc} p_{11} & p_{12} & \ldots ... ... p_{k1} & p_{k2} & \ldots & p_{k(n-k)} & 0 & 0 & \ldots & 1\end{array}}\right.$ $\displaystyle \begin{array}{cccccccc} p_{11} & p_{12} & \ldots & p_{1(n-k)} & 1... ...ts & 0\\ p_{k1} & p_{k2} & \ldots & p_{k(n-k)} & 0 & 0 & \ldots & 1\end{array}$ $\displaystyle \left.\vphantom{\begin{array}{cccccccc} p_{11} & p_{12} & \ldots ... ... p_{k1} & p_{k2} & \ldots & p_{k(n-k)} & 0 & 0 & \ldots & 1\end{array}}\right]$	(8.16)

Et donc

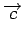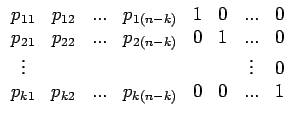$\displaystyle \overrightarrow{c}$ = (c₁, c₂,..., c_n) = (m₁, m₂,..., m_k) $\displaystyle \left[\vphantom{\begin{array}{cccccccc} p_{11} & p_{12} & ... & p... ... & 0\\ p_{k1} & p_{k2} & ... & p_{k(n-k)} & 0 & 0 & ... & 1\end{array}}\right.$ $\displaystyle \begin{array}{cccccccc} p_{11} & p_{12} & ... & p_{1(n-k)} & 1 & ... ...& \vdots & 0\\ p_{k1} & p_{k2} & ... & p_{k(n-k)} & 0 & 0 & ... & 1\end{array}$ $\displaystyle \left.\vphantom{\begin{array}{cccccccc} p_{11} & p_{12} & ... & p... ... & 0\\ p_{k1} & p_{k2} & ... & p_{k(n-k)} & 0 & 0 & ... & 1\end{array}}\right]$

(8.17)

tel que

c_i	=	m₁p_1i + m₂p_2i + ... + m_kp_ki		i = 1,...,(n - k)
	=	m_i-n+k		i = (n - k + 1),..., n

(8.18)

Finalement, le mot codé est constitué de bits de parité précédant le message

$\displaystyle \overrightarrow{c}$	=	$\displaystyle \underbrace{{p_{1},p_{2},...,p_{n-k},}}\,$	$\displaystyle \underbrace{{m_{1},m_{2},...,m_{k}}}\,$
		parit $\displaystyle \acute{{\textrm{e}}}$	message

(8.19)

Exemple. Dans le cas de MPEG,

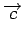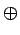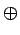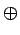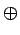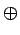$\displaystyle \overrightarrow{c}$ = (m₁ $\displaystyle \oplus$ m₂ $\displaystyle \oplus$ m₃, m₁ $\displaystyle \oplus$ m₂, m₁ $\displaystyle \oplus$ m₃, m₂ $\displaystyle \oplus$ m₃, m₁, m₂, m₃)

(8.20)

Cette expression permet de deviner les raisons qui ont conduit au choix des bits de parité. Les bits c₂, c₃, c₄ sont tels qu'on essaie d'isoler une erreur sur un bit du message. Le bit c₁ est lui plutôt destiné à indiquer des erreurs multiples.