Soit H la matrice appelée matrice de contrôle de parité,
destinée à permettre le contrôle d'erreur. Pour toute matrice G
de taille
(k×n), il existe une matrice H, de taille (n - k, n),
telle que les lignes de H soient orthogonales aux lignes de la
matrice G; autrement dit,
GHT = ![]() , où HT
est la transposée de la matrice H et
, où HT
est la transposée de la matrice H et
![]() une matrice
(k, n - k) dont tous les éléments sont nuls. Pour respecter la contrainte
d'orthogonalité, la matrice H a la forme
une matrice
(k, n - k) dont tous les éléments sont nuls. Pour respecter la contrainte
d'orthogonalité, la matrice H a la forme
| H = |
(8.21) |
| HT | = | 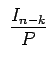 |
(8.22) |
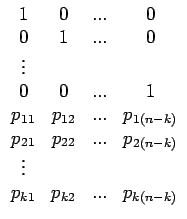 |
(8.23) |
On vérifie aisément que tout produit
![]() HT pour tout
HT pour tout
![]() généré au moyen de la matrice génératrice G fournit
un vecteur nul
généré au moyen de la matrice génératrice G fournit
un vecteur nul
Ce système d'équations fournit un outil précieux pour la détection
des erreurs de transmission lors du décodage en réception. En effet,
un mot codé
![]() a été généré par G si et seulement si
a été généré par G si et seulement si
![]() HT = 0.
HT = 0.