Table des matières of 8.5.1 Poids et distance de HAMMING

8.5.1 Poids et distance de HAMMING

La discussion précédente a clairement montré que toutes les erreurs ne pouvaient pas être corrigées. Avant de déterminer la capacité de correction d'un code, il faut pouvoir le caractériser.

Définition 46 Le poids de HAMMING w(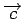 $\overrightarrow{c}$ ) du vecteur 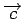$\overrightarrow{c}$ est le nombre de 1 qu'il contient.

Exemple. Voici le poids de deux vecteurs

w(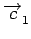 $\displaystyle \overrightarrow{c}_{{1}}^{}$ ) = w(100101101) = 5

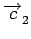w( $\displaystyle \overrightarrow{c}_{{2}}^{}$ ) = w(011110100) = 5

(8.32)

On peut aussi définir la distance entre deux vecteurs.

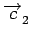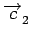Définition 47 Soient deux vecteurs binaires $\overrightarrow{c}_{{1}}^{}$ , $\overrightarrow{c}_{{2}}^{}$ , la distance de HAMMING d ( $\overrightarrow{c}_{{1}}^{}$ , $\overrightarrow{c}_{{2}}^{}$ ) est le nombre de bits qui diffèrent.

Reprenons l'exemple précédent. d ( 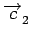$\overrightarrow{c}_{{1}}^{}$ , $\overrightarrow{c}_{{2}}^{}$ ) = 6. On montre aisément que poids et distance sont liés par la relation

d ( $\displaystyle \overrightarrow{c}_{{1}}^{}$ , $\displaystyle \overrightarrow{c}_{{2}}^{}$ ) = w( $\displaystyle \overrightarrow{c}_{{1}}^{}$ $\displaystyle \oplus$ $\displaystyle \overrightarrow{c}_{{2}}^{}$ )

(8.33)