Soit g(t) un signal non périodique. Par définition, la transformée
de FOURIER du signal g(t) est donnée par
À partir de la transformée de FOURIER, il est possible de
reconstituer exactement le signal original au moyen de la transformée
inverse :
Pour que la transformée d'un signal g(t) existe, il suffit (condition
suffisante mais pas nécessaire), que g(t) satisfasse les trois
conditions de DIRICHLET :
- La fonction g(t) est à valeur unique avec un nombre fini de maxima
et de minima pour tout intervalle fini.
- La fonction g(t) a un nombre fini de discontinuités pour tout intervalle
fini.
- La fonction est ``absolument'' intégrable, c'est-à-dire
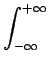 | g(t)| dt < | g(t)| dt < 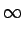 |
(A.3) |
La transformée de FOURIER nous fournit une interprétation
intéressante puisqu'elle décompose le signal en composantes fréquentielles
définies sur
[- 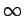 , +
, + 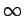 ].
].
Nous dirons que g(t) et
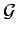 (f ) forment une paire
de transformées de FOURIER représentée par
(f ) forment une paire
de transformées de FOURIER représentée par
g(
t)
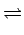
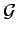
(
f )
En général,
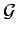 (f ) est une fonction de f à valeurs complexes.
Nous pouvons donc l'exprimer sous la forme
(f ) est une fonction de f à valeurs complexes.
Nous pouvons donc l'exprimer sous la forme
où
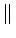
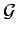 (f )
(f )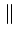 est appelé module de
est appelé module de
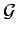 (f ) et
(f ) et 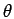 (f ) est appelée phase de
(f ) est appelée phase de
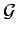 (f ).
Dans le cas particulier important où g(t) est une fonction à valeurs
réelles, nous avons
(f ).
Dans le cas particulier important où g(t) est une fonction à valeurs
réelles, nous avons
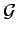 (- f )= (- f )= 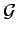 *(f ) *(f ) |
(A.5) |
où * représente le complexe conjugué. Il vient
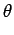 (- f )= - (- f )= - 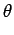 (f ) (f ) |
(A.7) |
Dès lors, nous pouvons déduire deux propriétés importantes d'un signal
à valeurs réelles :
- Le spectre d'amplitude du signal est une fonction paire de la fréquence,
c'est-à-dire que le spectre d'amplitude est symétrique par rapport
à l'axe vertical.
- Le spectre de phase du signal est une fonction impaire de la fréquence,
c'est-à-dire que le spectre de phase est antisymétrique par rapport
à l'axe vertical.
Marc Van Droogenbroeck. Tous droits réservés.
2004-06-11
![]() (f ) forment une paire
de transformées de FOURIER représentée par
(f ) forment une paire
de transformées de FOURIER représentée par
![]() (f ) est une fonction de f à valeurs complexes.
Nous pouvons donc l'exprimer sous la forme
(f ) est une fonction de f à valeurs complexes.
Nous pouvons donc l'exprimer sous la forme