En télécommunications, l'information d'une source est déterminante
au même titre que le temps nécessaire pour transmettre cette information.
En définitive, on cherche à transmettre un maximum d'information le
plus rapidement possible et en économisant au mieux les ressources
disponibles.
Définition 24
[Redondance] Pour indiquer l'écart entre l'entropie
d'une source et sa valeur maximale possible (lorsque tous les symboles
sont équiprobables), on définit la redondance
de la source
| RS = Hmax(S) - H(S) |
(4.18) |
où
Hmax(S) = log2n.
La redondance de la source est d'autant plus grande que son entropie
est faible, c'est-à-dire que l'incertitude liée à la source est faible.
Si certains symboles sont beaucoup plus probables que d'autres, l'entropie
de la source est faible et la source est dite redondante.
Marc Van Droogenbroeck. Tous droits réservés.
2004-06-11
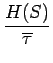 = H(S)
= H(S)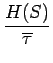 = H(S)
= H(S)