5.1.1 Hypothèses

Quel que soit le cas de figure, le signal modulant est supposé satisfaire aux deux exigences suivantes:

• Il est borné. D'où il existe une borne supérieure de l'amplitude du signal modulant

  $$\forall \left\vert\vphantom{x(t)}\right. \left.\vphantom{x(t)}\right\vert \leq$$ (5.1)

  
  
  À partir de cette hypothèse, il est commode de normaliser l'amplitude, en divisant la tension initiale par la valeur maximale, ce qui, somme toute, n'affecte pas l'information contenue dans le signal. Nous utiliserons donc un signal modulant normalisé m(t) défini par l'expression

  $${\frac{{x(t)}}{{x_{\max}}}}$$ (5.2)

  
  
  Cela étant, on peut encore distinguer
  • les signaux modulants non négatifs, comme les signaux vidéo ou les signaux binaires pour lesquels la tension est toujours positive.
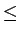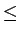  • les signaux modulants alternatifs, pour lesquels -1 $\leq$ m(t) $\leq$ 1. Appartiennent à cette catégorie, les signaux sonores ou les composantes de différence de couleur d'un signal vidéo.
    Le fait qu'un signal soit alternatif ne signifie pas pour autant qu'il ne contienne pas de composante continue. Pour s'en convaincre, il suffit de prendre un signal alternatif binaire pour lequel les deux états 0 et 1 ne seraient pas équiprobables. Mais comme la composante continue ne constitue pas un signal d'information intéressant et que sa présence entraîne un surcoût de puissance, on fait en sorte de la supprimer dans bon nombre d'applications. Les signaux sonores, les composantes de différence de couleur, et aussi la quasi-totalité des signaux modulants de nature composite sont dépourvus de composante continue.
• Le signal modulant m(t) est à spectre limité, c'est-à-dire qu'il existe une fréquence telle que la transformée de FOURIER du signal modulant, supposée existante, satisfasse à la condition

  $$\mathcal {M} \left\vert\vphantom{f}\right. \left.\vphantom{f}\right\vert$$ (5.3)

  
  
  On ne peut jamais imposer strictement cette condition puisqu'elle revient à exiger que le signal soit à durée infinie. C'est néanmoins une hypothèse raisonnable car les signaux réels ont des composantes spectrales négligeables au-delà d'une certaine fréquence. Du reste, sous peine d'effets indésirables d'intermodulation ou de saturation, on est presque toujours amené à traiter les signaux modulants par un filtrage passe-bas limitant leur spectre en entrée.

Définition 28   Dès lors que l'intervalle de fréquences est borné par la fréquence W, on appelle bande de base l'intervalle de fréquences [0, W].

Le fait que nous ayons à traiter des signaux réels n'est pas sans importance. En effet, leur transformée de FOURIER est telle que la partie réelle est paire et la partie imaginaire impaire; on dit alors que la transformée de FOURIER est paire, étant entendu qu'on considère le complexe conjugué. Cette propriété sera conservée tant qu'il s'agira d'un processus réalisable sur des signaux réels.