Définition 60
La densité spectrale de puissance
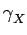 (f ) d'un processus
aléatoire stationnaire X(t) est la transformée de FOURIER
de sa fonction d'autocorrélation
(f ) d'un processus
aléatoire stationnaire X(t) est la transformée de FOURIER
de sa fonction d'autocorrélation
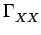
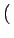
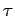
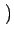 :
:
Ces relations sont appelées relations d'EINSTEIN-WIENER-KINTCHINE.
Voici quelques propriétés importantes de la densité spectrale de puissance:
Remarquons que la transformée de FOURIER d'un signal aléatoire
est elle-même aléatoire, et de ce fait, on ne peut pas la calculer.
On peut par contre déterminer sa densité spectrale de puissance car
cette fonction est déterministe -on suppose bien sûr la stationnarité
au sens large ainsi que l'ergodicité de X(t).
Exemple: onde sinusoïdale avec phase aléatoire.
Considérons un signal sinusoïdal avec phase aléatoire, défini
par
X(t) = Accos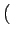 2 2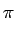 fct + fct + 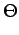 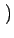 |
(4.118) |
où Ac et fc sont constants et 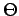 est une variable
aléatoire uniformément distribuée sur l'intervalle
est une variable
aléatoire uniformément distribuée sur l'intervalle
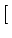 -
- 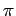 , +
, + 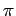
![$ \left.\vphantom{-\pi,+\pi}\right]$](img571.gif) ,
c'est-à-dire
,
c'est-à-dire
Calculons tout d'abord la moyenne statistique du processus aléatoire
X(t):
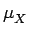 (t) (t) |
= |
E X(t) X(t) |
(4.120) |
| |
= |
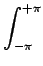 Accos Accos 2 2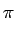 fct + fct +  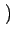 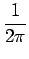 d d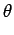 |
(4.121) |
| |
= |
0 |
(4.122) |
La moyenne statistique du processus aléatoire X(t) est donc indépendante
du temps. Évaluons maintenant sa fonction d'autocorrélation:
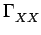  t1, t2 t1, t2 |
= |
E X(t1)X(t2) X(t1)X(t2) |
(4.123) |
| |
= |
E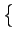 Ac2cos Ac2cos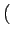 2 2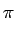 fct1 + fct1 + 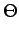 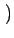 cos cos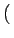 2 2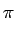 fct2 + fct2 + 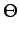   |
(4.124) |
| |
= |
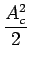 E E cos cos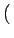 2 2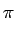 fc(t2 - t1) fc(t2 - t1)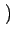 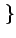 + + 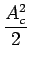 E E cos cos 2 2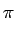 fc(t2 + t1) + 2 fc(t2 + t1) + 2 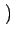 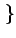 |
|
| |
= |
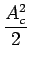 cos cos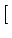 2 2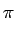 fc(t2 - t1) fc(t2 - t1)![$\displaystyle \left.\vphantom{2\pi f_{c}(t_{2}-t_{1})}\right]$](img597.gif) |
(4.125) |
Il apparaît que la fonction d'autocorrélation du processus aléatoire
X(t) dépend exclusivement de la différence entre les temps d'observation
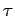 = t2 - t1. Nous pouvons donc écrire
= t2 - t1. Nous pouvons donc écrire
Étant donné que la moyenne statistique de X(t) ne dépend pas du
temps et que sa fonction d'autocorrélation ne dépend que de la différence
entre les temps d'observation, nous pouvons conclure que le processus
aléatoire X(t) est stationnaire au sens large. Évaluons à présent
la densité spectrale de puissance de X(t):
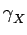 (f )= (f )= 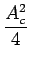 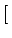  (f - fc) + (f - fc) +  (f + fc) (f + fc)![$\displaystyle \left.\vphantom{\delta(f-f_{c})+\delta(f+f_{c})}\right]$](img153.gif) |
(4.127) |
qui est constituées de deux raies situées en
f = ±fc et pondérées
par le facteur
Ac2/4. Notons que l'aire totale sous le graphe
de
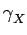 (f ) est égale à
Ac2/2, ce qui correspond bien
à
E
(f ) est égale à
Ac2/2, ce qui correspond bien
à
E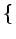 X2(t)
X2(t)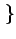 =
= 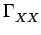
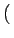 0
0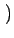 .
.
Marc Van Droogenbroeck. Tous droits réservés.
2005-03-11
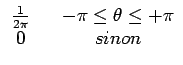
![]() = t2 - t1. Nous pouvons donc écrire
= t2 - t1. Nous pouvons donc écrire