8.2.3 Processus de POISSON

Prenons un intervalle de temps ]t₀, t₁] . Le nombre d'occurrences pendant cet intervalle de temps est fourni par la loi de POISSON avec T = t₁ - t₀ . Ce résultat s'appuie sur le fait que les tirages que représente la loi binomiale sont indépendants entre eux. Dès lors, les occurrences relevées sur des intervalles de temps sans recouvrement sont indépendants. À la limite, lorsque T 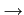$\rightarrow$ 0 , le dénombrement résulte d'une succession d'observations indépendantes, toutes décrites par une loi de POISSON. Il s'agit dans ce cas d'un processus de POISSON.

Définition 32   [Processus de POISSON] Un processus de dénombrement D(t) est un processus de POISSON d'intensité 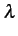$\lambda$ s'il respecte la double condition suivante
(1) le nombre d'occurrences durant tout intervalle de temps ]t₀, t₁] , D(t₁) - D(t₀) , est une variable aléatoire de POISSON d'espérance 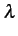$\lambda$(t₁ - t₀) , et
(2) pour toute paire d'intervalle ]t₀, t₁] , ]t₂, t₃] , le nombre d'occurrences durant ces intervalles, D(t₁) - D(t₀) et D(t₃) - D(t₂) , sont des variables aléatoires indépendantes.