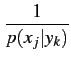Pour un canal bruité, la question posée est de savoir quelle incertitude
subsiste sur l'entrée X
après avoir observé la sortie Y = yk
.
Pour répondre à cette question, définissons l'entropie de X
conditionnellement
à Y
, sachant que Y = yk
de la manière suivante
H(X| Y = yk) =  p(xj| yk) log2 p(xj| yk) log2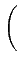 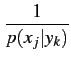 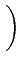 |
(9.94) |
Cette formule nous donne dès lors l'incertitude subsistant sur la
valeur de l'entrée connaissant la valeur yk
de la sortie. Il
serait intéressant d'avoir une moyenne de cette information pour toutes
les valeurs de Y
et donc pour toutes les sorties possibles, c'est
l'entropie conditionnelle H(X| Y)
,
donnée par
| H(X| Y) |
= |
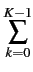 H(X| Y = yk)p(yk) H(X| Y = yk)p(yk) |
(9.95) |
| |
= |
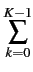  p(xj| yk)p(yk) log2 p(xj| yk)p(yk) log2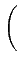 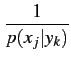 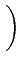 |
(9.96) |
| |
= |
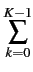  p(xj, yk) log2 p(xj, yk) log2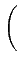 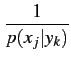  |
(9.97) |
On définit alors l'information mutuelle
moyenne I(X;Y)
comme la quantité d'information, et donc d'entropie,
que l'on retrouve en sortie du canal (et donc qui n'a pas été affecté
par le bruit). Dès lors,
| I(X;Y) = H(X) - H(X| Y) |
(9.98) |
On peut illustrer cette définition dans deux cas particuliers:
- le cas d'un canal sans bruit. Alors, H(X| Y) = 0
car connaissant le symbole de sortie, il est possible de déterminer
avec certitude le symbole d'entrée. Aussi
I(X;Y) = H(X)
: le canal
arrive donc bien à véhiculer l'information jusqu'au récepteur.
- le cas d'un canal fortement bruité au point que
tous les symboles soient équiprobables. Alors
H(X| Y) = H(X)
, car
l'analyse de la sortie ne permet pas d'obtenir la moindre information
sur l'entrée. Ainsi donc, I(X;Y)
est nulle; le canal ne transmet
aucune information.
On peut montrer que l'information mutuelle moyenne possède notamment
la propriété d'être symétrique, dès lors
I(X;Y) = I(Y;X)
, on en déduit
que
| I(X;Y) |
= |
H(X) - H(X| Y) |
(9.99) |
| I(Y;X) |
= |
H(Y) - H(Y| X) |
(9.100) |
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27