10.2.3 Affaiblissement de parcours

Tout comme dans le cas d'une liaison en espace libre, si la distance d entre l'émetteur et le récepteur augmente la surface apparente de l'antenne de réception diminue, ce qui se traduit par un accroissement de l'atténuation. En ligne de vue et en l'absence de réflexion, l'affaiblissement, appelé affaiblissement de parcours ou path loss, est proportionnel au carré de la distance d² . Comme cette hypothèse n'est que rarement vérifiée en pratique, l'affaiblissement est proportionnel à une puissance supérieure de d . On opte, par exemple, pour une valeur médiane de l'affaiblissement valant d^{3, 5} .

L'affaiblissement fournit une évolution de la puissance qui, localement, peut s'écarter des valeurs moyennes observées. En effet, prenons le cas d'une communication GSM à 900 [MHz] , entre une antenne d'émission et un mobile distant de 1 [km] . Suivant la loi d'affaiblissement en d^{3, 5} , s'écarter de 1 [m] contribue à une augmentation de l'affaiblissement de 35 x (log₁₀1001 - log₁₀1000) , soit 0, 015 [dB] . Or, la longueur d'onde correspondant à 900 [MHz] est 0, 33 [m] . Autrement dit, parcourir une distance de 1 [m] équivaut à 3 longueurs d'onde. À supposer qu'une paroi réfléchisse parfaitement le signal émis, le mobile reçoit le signal direct et le signal réfléchi avec des phases respectives qui peuvent aller de la concordance de phase à l'opposition de phase, soit un affaiblissement supplémentaire allant de -6 [dB] à + 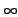$\infty$ [dB] . Ces différents cas de figure peuvent donc se produire plusieurs fois sur une distance de 1 [m] .

En définitive, c'est l'allure de l'affaiblissement que l'on traite avec une loi qui serait fonction de la distance; à ce titre, la valeur fournie par les modèles empiriques est la valeur médiane des valeurs observées. Il faut ajouter à cela des effets statistiques de masquage et de phase.