A.3 Adaptation d'impédance

Considérons une force électromotrice sinusoïdale d'amplitude V et d'impédance interne $\widehat{{Z}}_{{s}}^{}$ . Relions ses bornes à celles d'un circuit d'utilisation d'impédance $\widehat{{Z}}_{{L}}^{}$ , et cherchons la valeur de $\widehat{{Z}}_{{L}}^{}$ pour laquelle la puissance moyenne fournie au circuit est maximale. En posant $\widehat{{Z}}_{{s}}^{}$ = R_s + jS_s et $\widehat{{Z}}_{{L}}^{}$ = R_L + jS_L , on montre aisément que la puissance moyenne dissipée P_d dans la charge est maximale lorsque R_s = R_L et S_s = S_L , soit lorsque

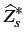$$\widehat{{Z}}_{{L}}^{} \widehat{{Z}}_{{s}}^{{\ast}}$$ (A.15)

On dit alors que l'impédance du circuit d'utilisation est adaptée à celle du générateur. La puissance fournie est maximale et vaut

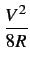$${\frac{{V^{2}}}{{8R}}}$$ (A.16)

Notons qu'une puissance égale est dissipée dans le générateur, ce qui diminue pour de nombreuses applications l'intérêt de cette adaptation.