; cette quantité est non
aléatoire.
À partir des échantillons
{x[0], x[1], ..., x[N - 1]}
,
on calcule une certaine estimation notée
 . Cette
estimation est donc une fonction A
des échantillons
. Cette
estimation est donc une fonction A
des échantillons
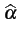 = A(x[0], x[1], ..., x[N - 1]) = A(x[0], x[1], ..., x[N - 1]) |
(1.40) |
La fonction A
est appelée estimateur
de 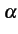 ;
;
 est l'estimation.
est l'estimation.
Contrairement à 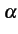 , l'estimation
, l'estimation
 est
une variable aléatoire puisqu'elle fait intervenir les échantillons
d'une séquence aléatoire. À ce titre, elle possède une certaine densité
de probabilité, une moyenne, une variance, etc.
est
une variable aléatoire puisqu'elle fait intervenir les échantillons
d'une séquence aléatoire. À ce titre, elle possède une certaine densité
de probabilité, une moyenne, une variance, etc.
Ce problème est différent des problèmes rencontrés en statistique
car il s'agit d'estimer une fonction et non une série de paramètres.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]()
![]() = A(x[0], x[1], ..., x[N - 1])
= A(x[0], x[1], ..., x[N - 1])![]()
![]()
![]()
![]()