- le biais. Le biais est défini par
b 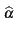 =
= 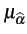 -
- 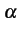
(1.41)
Un estimateur de biais nul est dit non biaisé. - la variance de l'estimateur, qui est celle de la variable

, soit 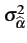 = E
= E (
(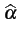 -
- 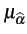 )2
)2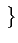
(1.42)
- l'erreur quadratique moyenne (Mean Square Error). Il
s'agit de la quantité
MSE 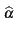 = E
= E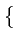 (
(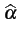 -
- 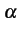 )2
)2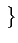
(1.43)
On montre aisément queMSE 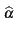 = b
= b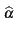 2 +
2 + 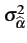
(1.44)
On parle d'estimateur consistant si son
erreur quadratique moyenne tend vers 0
Cette condition, à mettre en parallèle avec l'ergodisme, est essentielle
quand il s'agit d'exploiter les données d'échantillons prélevés sur
une longue période.
![]() MSE
MSE![]() = 0
= 0
(1.45)
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27