1.4.4 Effet de fenêtrage

On peut aussi s'intéresser à la forme de la fonction fenêtre que l'on applique. En effet,

$$\widehat{{\gamma }}_{{X}}^{} {\frac{{1}}{{N}}} \left\Vert\vphantom{ \sum_{n=0}^{N-1}x[n]e^{-2\pi jFn}}\right. \sum_{{n=0}}^{{N-1}} \pi \left.\vphantom{ \sum_{n=0}^{N-1}x[n]e^{-2\pi jFn}}\right\Vert^{{2}}_{}$$ = (1.76)

$${\frac{{1}}{{N}}} \left\Vert\vphantom{ \sum_{n=-\infty}^{+\infty}x[n]w_{R}[n]e^{-2\pi jFn}}\right. \sum_{{n=-\infty}}^{{+\infty}} \pi \left.\vphantom{ \sum_{n=-\infty}^{+\infty}x[n]w_{R}[n]e^{-2\pi jFn}}\right\Vert^{{2}}_{}$$ = (1.77)

où w_R[n] est une fonction de fenêtrage de forme rectangulaire définie par

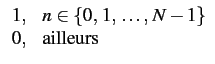$$\left\{\vphantom{ \begin{array}{ll} 1, & n\in\{0, 1, \ldots, N-1\} 0, & \textrm{ailleurs}\end{array}}\right. \begin{array}{ll} 1, & n\in\{0, 1, \ldots, N-1\} 0, & \textrm{ailleurs}\end{array}$$ (1.78)

L'effet de la fenêtre n'est pas négligeable car il affecte le spectre du signal observé. Aussi, différentes méthodes d'estimation spectrale tentent-elles d'établir un compromis entre précision spectrale et effet de fenêtrage.

La question de l'estimation spectrale est trop vaste pour que nous l'abordions autrement que par une sensibilisation à la difficulté intrinsèque à estimer un spectre. Pour une étude approfondie, nous renvoyons le lecteur intéressé à des ouvrages spécialisés [5,6,14].