- les modulations linéaires pour
lesquelles
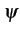
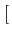 m(t)
m(t)![$ \left.\vphantom{m(t)}\right]$](img498.gif)
est une fonction linéaire de m(t) . - les modulations angulaires pour
lesquelles
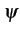
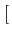 m(t)
m(t)![$ \left.\vphantom{m(t)}\right]$](img498.gif)
a la forme 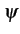
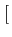 m(t)
m(t)![$\displaystyle \left.\vphantom{m(t)}\right]$](img492.gif) = ej
= ej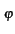
 m(t)
m(t)![$\scriptstyle \left.\vphantom{m(t)}\right]$](img503.gif)
(4.2)
où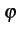
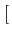 m(t)
m(t)![$ \left.\vphantom{m(t)}\right]$](img498.gif)
est une fonction linéaire de m(t) .
qui met en évidence la composante en phase
qui, cette fois, met en évidence l'enveloppe et la phase du signal modulé.
Par la suite, nous nous concentrerons essentiellement sur les modulations numériques linéaires qui s'expriment par
où les signaux dk(t)
- les modulations ``classiques'', pour lesquelles
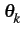 = 2
= 2 fckT
fckT
, et - les modulations à décalage (ou
offset), pour lesquelles
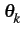 = 2
= 2 fckT + k
fckT + k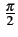
.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27