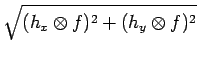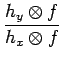Par commodité, nous considérons une image caractérisée par une fonction
f (x, y) bidimensionnelle et continue. Il faut, dans ce cas, indiquer
dans quelle direction on calcule la dérivée. Les principaux
choix sont les directions horizontale
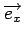 ou verticale
ou verticale
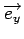 ; une dérivée dans une autre direction
; une dérivée dans une autre direction
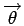 peut se ramener à une combinaison des dérivées suivant les axes principaux
-il s'agit alors de dérivée directionnelle.
peut se ramener à une combinaison des dérivées suivant les axes principaux
-il s'agit alors de dérivée directionnelle.
Considérons la dérivée partielle
de la fonction f (x, y) par rapport à x La transformée de FOURIER
de cet opérateur vaut
Dériver par rapport à x équivaut donc à multiplier la transformée
de FOURIER de f (x, y) par la fonction de transfert
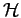 x(u, v) = 2
x(u, v) = 2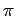 ju,
c'est-à-dire filtrer f (x, y) avec le filtre dont la réponse impulsionnelle
est donnée par
ju,
c'est-à-dire filtrer f (x, y) avec le filtre dont la réponse impulsionnelle
est donnée par
hx(x, y) =   (2 (2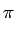 ju) e2 ju) e2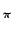 j(xu+yv)dudv j(xu+yv)dudv |
(6.2) |
De même, on peut définir la réponse impulsionnelle
hy(x, y) correspondant
au filtrée dérivée dans la direction
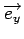 . Le module
de la fonction de transfert
. Le module
de la fonction de transfert
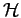 x(u, v) étant égal à 2
x(u, v) étant égal à 2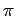 | u|,
on voit clairement qu'il y a un effet accentuateur des hautes fréquences,
d'où le caractère passe-haut de l'opérateur dérivée. C'est pareil
pour
hy(x, y).
| u|,
on voit clairement qu'il y a un effet accentuateur des hautes fréquences,
d'où le caractère passe-haut de l'opérateur dérivée. C'est pareil
pour
hy(x, y).
En adoptant une notation vectorielle de la dérivée, on définit le
gradient
 f de l'image f par
f de l'image f par
 f = f = 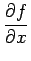 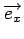 + + 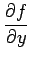 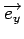 = (hx = (hx 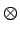 f ) f )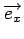 + (hy + (hy 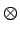 f ) f )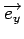 |
(6.3) |
Le gradient d'une fonction f (x, y) est une fonction vectorielle.
Mais plutôt que de recourir aux composantes en x et y, on peut
caractériser un gradient par son amplitude et sa direction.
Définition 52
[Amplitude du gradient]
Remarque pratique: approximation du gradient
On approxime parfois l'amplitude du gradient (ou d'une norme) par
l'expression
pour éviter le calcul de la racine carrée et les élévations au carré
afin d'accélérer le calcul mais cette formule n'est qu'une approximation.
Cette approximation est tout à fait raisonnable lorsqu'un terme dépasse
largement l'autre. Par exemple, si
hx 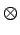 f
f 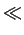 hy
hy 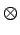 f,
f,
 f
f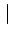
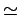
 hy
hy 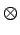 f
f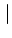 . Dans le
cas où les deux termes sont d'amplitude égale, on a
. Dans le
cas où les deux termes sont d'amplitude égale, on a
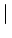
 f
f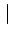
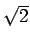
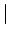 hx
hx 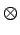 f
f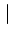 .
L'erreur peut donc atteindre 41%.
.
L'erreur peut donc atteindre 41%.
Définition 53
[Direction du gradient]
Étant donnée la définition du gradient d'une fonction, il est
maintenant possible de définir sa dérivée directionnelle par
Définition 54
[Dérivée directionnelle]
Il s'agit du produit scalaire du gradient de f et d'un vecteur
caractérisant la direction dans laquelle on désire calculer la dérivée.
Si la direction
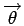 fait un angle
fait un angle 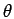 avec l'axe
x, c'est-à-dire
avec l'axe
x, c'est-à-dire
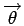 = cos
= cos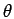
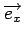 + sin
+ sin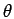
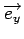 ,
la dérivée directionnelle peut encore s'écrire
,
la dérivée directionnelle peut encore s'écrire
Pour 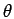 = 0, nous retrouvons la dérivée directionnelle dans la
direction
= 0, nous retrouvons la dérivée directionnelle dans la
direction
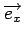 . La dérivée directionnelle est utile
pour mettre en évidence les contours d'une image qui ont une orientation
particulière.
. La dérivée directionnelle est utile
pour mettre en évidence les contours d'une image qui ont une orientation
particulière.
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30
![]() ou verticale
ou verticale
![]() ; une dérivée dans une autre direction
; une dérivée dans une autre direction
![]() peut se ramener à une combinaison des dérivées suivant les axes principaux
-il s'agit alors de dérivée directionnelle.
peut se ramener à une combinaison des dérivées suivant les axes principaux
-il s'agit alors de dérivée directionnelle.
![]() f de l'image f par
f de l'image f par