Si les matrices de transformation
![]() et
et
![]() sont des matrices de HADAMARD, alors
sont des matrices de HADAMARD, alors
![]() =
= ![]()
![]()
![]() est appelée transformée de HADAMARD de l'image
est appelée transformée de HADAMARD de l'image
![]() .
Une matrice de HADAMARD
.
Une matrice de HADAMARD
![]() est une matrice
symétrique, de dimension J×J, dont les éléments sont tous
égaux à ±1 et définie comme suit. La matrice d'HADAMARD
du second ordre est
est une matrice
symétrique, de dimension J×J, dont les éléments sont tous
égaux à ±1 et définie comme suit. La matrice d'HADAMARD
du second ordre est
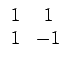 |
(2.22) |
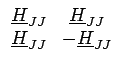 |
(2.23) |
| (2.24) |
Étant donnée la composition des matrices de transformation, la transformée de HADAMARD et son inverse peuvent être calculée uniquement par des additions. La transformée de HADAMARD est parfois appelée transformée de WALSH-HADAMARD. Elle est occasionnellement utilisée dans des applications de codage d'images.