La transformée de FOURIER d'une image
f x, y
x, y est définie par
est définie par
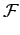  u, v u, v = =   f f x, y x, y e-2 e-2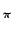 j j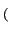 xu + yv xu + yv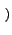 dxdy dxdy |
(2.33) |
où u et v désignent les fréquences spatiales dans les directions
x et y. À partir de la transformée de FOURIER, il est
possible de reconstituer exactement l'image originale en prenant la
transformée inverse
f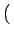 x, y x, y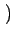 = =   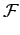  u, v u, v e2 e2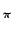 j j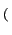 ux + vy ux + vy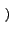 dudv dudv |
(2.34) |
Pour que la transformée d'une image existe, la condition suivante
suffit
La transformée de FOURIER nous fournit une interprétation
intéressante puisqu'elle décompose l'image en composantes fréquentielles
définie sur
 -
- 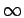 , +
, + 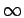
![$ \left.\vphantom{-\infty,+\infty}\right]$](img247.gif) ×
× -
- 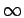 , +
, + 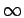
![$ \left.\vphantom{-\infty,+\infty}\right]$](img247.gif) .
f
.
f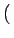 x, y
x, y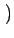 et
et
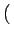 u, v
u, v forment une
paire de transformée de FOURIER représentée par
forment une
paire de transformée de FOURIER représentée par
En général,
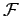
 u, v
u, v est une fonction de u
et de v à valeurs complexes. Nous pouvons donc l'exprimer sous
la forme
est une fonction de u
et de v à valeurs complexes. Nous pouvons donc l'exprimer sous
la forme
où
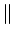
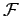
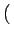 u, v
u, v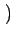
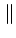 est appelé module
de
est appelé module
de
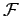
 u, v
u, v ou spectre
fréquentiel de l'image
f
ou spectre
fréquentiel de l'image
f x, y
x, y et
et
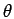
 u, v
u, v est la phase de
est la phase de
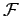
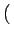 u, v
u, v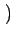 ou spectre de phase de
ou spectre de phase de
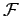
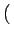 u, v
u, v . Dans
le cas particulier important où
f
. Dans
le cas particulier important où
f x, y
x, y est une fonction
à valeurs réelles, nous avons
est une fonction
à valeurs réelles, nous avons
Dès lors,
On peut en déduire deux propriétés importantes d'une image à valeurs
réelles:
- le spectre fréquentiel de l'image est symétrique par rapport à l'origine
du système d'axes u - v. C'est-à-dire que la connaissance d'un demi-plan
suffit. Ce résultat est satisfaisant car si, dans le plan spatial,
on dispose de M×N variables indépendantes, la transformée
de FOURIER fournit seulement
(M×N)/2 variables indépendantes
mais ces variables sont complexes.
- le spectre de phase de l'image est anti-symétrique par rapport à l'origine
du système d'axes u - v.
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30
![]() x, y
x, y![]() est définie par
est définie par ![]() -
- ![]() , +
, + ![]()
![]() ×
×![]() -
- ![]() , +
, + ![]()
![]() .
f
.
f![]() x, y
x, y![]() et
et
![]()
![]() u, v
u, v![]() forment une
paire de transformée de FOURIER représentée par
forment une
paire de transformée de FOURIER représentée par ![]()
![]() u, v
u, v![]() est une fonction de u
et de v à valeurs complexes. Nous pouvons donc l'exprimer sous
la forme
est une fonction de u
et de v à valeurs complexes. Nous pouvons donc l'exprimer sous
la forme