L'extension des outils de la morphologie mathématique à l'étude des images en niveaux de gris s'est réalisée longtemps après la définition des concepts de la théorie. MEYER et STERNBERG [36] furent les véritables initiateurs de techniques adaptées à des images en niveaux de gris.
Soit
![]() un ensemble de valeurs de niveaux de gris. Dans
ce qui suit, nous supposerons que
un ensemble de valeurs de niveaux de gris. Dans
ce qui suit, nous supposerons que
![]() est un espace complété
(
est un espace complété
(
![]() =
= ![]()
![]() { -
{ - ![]() , +
, + ![]() } ou
} ou
![]() =
= ![]()
![]() { -
{ - ![]() , +
, + ![]() }).
Une image est représentée par une fonction
f :
}).
Une image est représentée par une fonction
f : ![]()
![]()
![]() ,
qui à tout point du plan fait correspondre une valeur. En pratique,
l'image n'est pas définie sur la totalité du référentiel
,
qui à tout point du plan fait correspondre une valeur. En pratique,
l'image n'est pas définie sur la totalité du référentiel
![]() mais sur un support compact D qui constitue la partie visible de
l'image. Néanmoins, à condition de bien comprendre les effets de bord,
rien ne nous empêche de considérer une support infini par facilité.
mais sur un support compact D qui constitue la partie visible de
l'image. Néanmoins, à condition de bien comprendre les effets de bord,
rien ne nous empêche de considérer une support infini par facilité.
Pour la morphologie mathématique en niveaux de gris, les opérations
de base ne sont plus l'union et l'intersection mais le supremum
![]() et l'infimum
et l'infimum ![]() . Pour aborder le cadre
algébrique, il faut d'abord définir la notion d'ordre entre fonctions,
tout comme nous l'avions fait pour les ensembles en utilisant la notion
d'inclusion.
. Pour aborder le cadre
algébrique, il faut d'abord définir la notion d'ordre entre fonctions,
tout comme nous l'avions fait pour les ensembles en utilisant la notion
d'inclusion.
| f |
(4.36) |
Insistons bien sur le fait que a fonction f est inférieure (![]() )
à la fonction g si, en tout point x de
)
à la fonction g si, en tout point x de
![]() , on a
l'inégalité de valeur
f (x)
, on a
l'inégalité de valeur
f (x) ![]() g(x). Comme toutes les valeurs d'une
fonction ne sont pas nécessairement toutes inférieures ou supérieures
à une autre fonction, il n'est pas toujours possible de déterminer
l'ordre entre des fonctions; c'est la raison pour laquelle il s'agit
d'un ordre partiel.
g(x). Comme toutes les valeurs d'une
fonction ne sont pas nécessairement toutes inférieures ou supérieures
à une autre fonction, il n'est pas toujours possible de déterminer
l'ordre entre des fonctions; c'est la raison pour laquelle il s'agit
d'un ordre partiel.
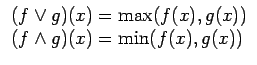 |
(4.37) |
Tout comme pour des ensembles, il nous reste à définir le translaté d'une fonction.
| (4.38) |