Les opérateurs morphologiques de fonctions agissent comme des transformations
d'ensembles. Dans ce paragraphe, nous étendons les concepts vus précédemment
aux opérateurs de fonctions.
Définition 32
[Idempotence]
Une transformation 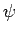 est idempotente si, quelle que soit
la fonction traitée, une nouvelle application de l'opérateur n'apporte
aucun changement, c'est-à-dire si
est idempotente si, quelle que soit
la fonction traitée, une nouvelle application de l'opérateur n'apporte
aucun changement, c'est-à-dire si
Définition 33
[Extensivité]
Un opérateur est extensif si la fonction transformée est plus grande
que la fonction de départ
Définition 34
[Anti-extensivité] Une transformation de fonctions
est anti-extensive si la fonction transformée est plus petite que
la fonction de départ
La croissance est une autre propriété qui joue un rôle primordial
dans les traitements morphologiques. Elle indique si un opérateur
préserve la relation d'ordre.
Par extension aussi, une transformation 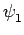 est inférieure
à un transformation
est inférieure
à un transformation 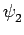 si, pour toute fonction f,
si, pour toute fonction f,
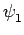 (f )
est inférieur à
(f )
est inférieur à
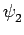 (f ):
(f ):
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30