2.4.3 Notion d'entropie

La théorie mesure la redondance en comparant la taille initiale à l'entropie du message. Voici la définition de cette dernière.

Définition 19   [Entropie] Soit un alphabet X de N lettres, l'entropie de cet alphabet, noté H(X), est l'opposé de la somme du produit des probabilités multipliées par leur logarithme en base 2

$$\sum_{{n=1}}^{{N}}$$ (2.11)

L'entropie est exprimée en bits, ce qui signifie que l'entropie est calculée par le logarithme en base binaire. Pour un alphabet de deux lettres de même probabilité, le calcul de H(X) fournit un bit^2.6, parfois appelé Shannon. L'entropie est donc telle qu'il faut un bit pour discerner entre les deux lettres.

Le tableau suivant compare l'entropie de deux alphabets dont les lettres ont des probabilités différentes.

A	:	0.25		A	:	0.7
B	:	0.25		B	:	0.1
C	:	0.25		C	:	0.1
D	:	0.25		D	:	0.1
H(X)	=	2 bits		H(Y)	=	1,4 bits

L'entropie mesure l'incertitude quant à une valeur. Dans la partie gauche du tableau, les quatre lettres sont équiprobables; on ne peut donc prévoir quelle lettre sera vraisemblablement choisie lors d'un prochain tirage au sort. De la sorte, il n'y a pas moyen de distinguer entre les quatre lettres et par conséquent l'entropie vaut 2 bits. Dans la partie droite, le déséquilibre entre les probabilités est net: la lettre A est plus probable que les autres lettres, ce qui entraîne une diminution de l'entropie.

On montre que l'entropie est maximale et vaut log₂n lorsque tous ses symboles d'une source sont équiprobables. En effet, prenons le cas d'une source binaire comprenant les deux symboles x₁ et x₂, telle que

$$\left\{\vphantom{ \begin{array}{c} p(x_{1})=k\\ p(x_{2})=1-k\end{array}}\right.$$$$\begin{array}{c} p(x_{1})=k\\ p(x_{2})=1-k\end{array}$$

où k $\in$ $\left[\vphantom{0,1}\right.$0, 1$\left.\vphantom{0,1}\right]$. L'entropie de cette source vaut, par définition,

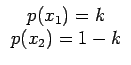
H(S) = - k log₂k - (1 - k)log₂(1 - k) (2.12)

L'entropie est une fonction de la probabilité k. Notons, par soucis de clarté, la valeur de l'entropie de source comme une fonction de son argument H(k). Cette fonction est représentée à la figure 2.30.

Figure 2.30: Entropie d'une source binaire en fonction de la probabilité de ses symboles.

 

On peut tout d'abord remarquer que l'entropie est nulle pour k = 1 (le symbole x₁ est émis avec certitude) et pour k = 0 (le symbole x₂ est émis avec certitude), ce qui correspond au cas où il n'y a aucune incertitude sur le symbole émis par la source. De plus, l'entropie atteint son maximum pour k = 0, 5 -la source a alors une entropie d'information de 1 [b/symbole]- , ce qui correspond au fait que les deux symboles sont équiprobables. En d'autres mots, il est tout aussi probable que la source émette le symbole x₁ que le symbole x₂.

Notes

... bit^2.6

On devrait, en principe, parler de bit d'information pour le distinguer de l'unité de mesure du débit.