| s0(t) | = | - 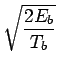 cos(2 cos(2 |
(7.7) |
| s1(t) | = | - 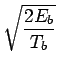 cos(2 cos(2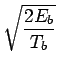 cos(2 cos(2 |
(7.8) |
En modulation de phase numérique cohérente, appelée Phase-Shift
Keying (PSK), on agit sur la phase de la porteuse.
Il y a autant d'états de phase différents qu'il y a de niveaux distincts
dans l'alphabet d'émission. Considérons le cas d'une PSK binaire (BPSK).
Cette modulation définit les deux états suivants
| s0(t) | = | - 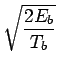 cos(2 cos(2 |
(7.7) |
| s1(t) | = | - 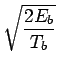 cos(2 cos(2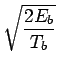 cos(2 cos(2 |
(7.8) |
L'occupation spectrale d'une modulation de phase cohérente binaire est identique à celle d'une modulation d'amplitude à deux états. Pour s'en convaincre, il suffit de choisir une modulation d'amplitude telle que A0 = - A1. Les conclusions obtenues précédemment s'appliquent donc également au cas de la PSK à deux états.
La démodulation d'un signal PSK peut se faire de différentes manières. Dans le cas de la démodulation cohérente, on peut montrer que