Le canal binaire symétrique est un cas particulier de canal discret
sans mémoire. Les alphabets d'entrée et de sortie se limitent aux
deux caractères 0 et 1. De plus, les probabilités conditionnelles
sont symétriques
| p(0| 1) | = | p(1| 0) = p | |
| p(1| 1) | = | p(0| 0) = 1 - p |
Sur base d'un modèle de ce type, on définit aisément la probabilité d'erreur d'un démodulateur. Dans le cas d'une modulation de phase à deux états, on établit que la probabilité d'erreur Pe vaut
Pe = 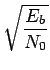 |
(8.1) |
La démodulation comprenant le filtre adapté suivi d'un organe de décision est relativement contraignante car elle s'effectue statiquement sur base d'un seuil.
On peut généraliser la notion de canal discret sans mémoire en prenant
le même alphabet d'entrée discret à M niveaux, mais en considérant
que la sortie est continue sur l'intervalle
[- ![]() , +
, + ![]() ].
Cette modélisation permet de considérer que le canal ajoute du bruit
au signal. Soit donc un bruit gaussien de moyenne nulle et de variance
].
Cette modélisation permet de considérer que le canal ajoute du bruit
au signal. Soit donc un bruit gaussien de moyenne nulle et de variance
![]() , la densité de probabilité de la variable aléatoire
de sortie z, liée à la valeur estimée uk, issue du filtre
adapté, est
, la densité de probabilité de la variable aléatoire
de sortie z, liée à la valeur estimée uk, issue du filtre
adapté, est
p(z| uk) = 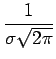 e- e- |
(8.2) |
Quand l'organe de décision dispose des densités de probabilité pour toutes les valeurs d'entrée, il est en mesure de prendre une décision plus souple sur le symbole transmis mais ce type de décision est plus complexe.
Dans notre cas, nous prendrons le schéma usuel de décision, à savoir celui qui consiste à établir les décisions sur base de seuils fixés une fois pour toutes.