8.3.1 Un exemple simple: code redondant

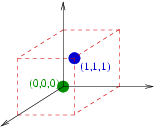
Prenons le cas d'une source binaire. On peut par exemple décider de tripler les symboles d'émission. Ainsi, 0 et 1 deviennent respectivement 000 et 111. Comme le montre la figure 8.1, l'effet du triplement peut s'interpréter comme le passage d'un espace à une dimension à un espace à trois dimensions. Néanmoins, en l'absence de toutes erreurs, seuls les états (0, 0, 0) et (1, 1, 1) sont possibles.

Figure 8.1: Interprétation d'un code redondant dans un espace à 3 dimensions.

 

Après transmission, il se peut fort bien que le récepteur obtienne un triplet erroné, comme (0, 0, 1). Dans ce cas d'erreur simple^8.1, le décodeur peut opérer une correction par vote majoritaire. Ce type de correction est illustré à la figure 8.2.

Figure 8.2: Possibilité de corrections d'erreurs simples par vote majoritaire.

 

Dans le cas d'erreurs doubles ou triples, la correction par vote majoritaire ne permet pas d'obtenir la valeur correcte du bit d'information généré par la source. En conséquence, on observe que le codage par triplement permet seulement certaines corrections; ces corrections se traduisent pas une diminution de la probabilité d'erreur sur bit d'information de la source. Remarquons au passage que le codage par doublement n'aurait permis aucune correction d'erreur.

Notes

...simple^8.1

Une erreur est dite simple lorsque seul un bit est incorrect.