Table des matières of 8.3.4 Codes à parité

8.3.4.1 Codes à détection de parité simple

8.3.4 Codes à parité

8.3.4.1 Codes à détection de parité simple

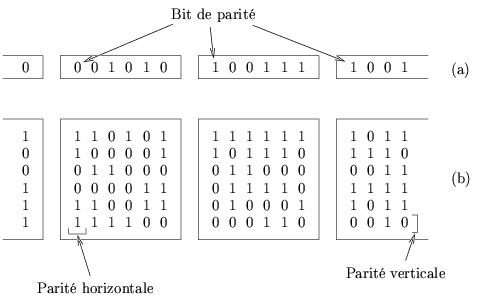
Les codes à parité simple se contentent d'ajouter un bit de parité pour la détection ou correction d'erreur. La valeur de la parité est calculée de manière à assurer que la somme des bits du message plus le bit de parité soit égale à 1, on parle alors de parité impaire, ou égale à 0, il s'agit dans ce cas de parité paire. La figure 8.3 montre le principe des codes de parité paire pour des transmissions série et parallèle.

**Figure 8.3:** Codes de parité paire pour (a) connexion série ou (b) parallèle.

Le récepteur se charge de vérifier si la parité est respectée. Si la parité n'est pas respectée, le récepteur peut en déduire la présence d'une erreur. L'erreur peut être de plusieurs types:

bit de parité erroné,
bit du message erroné, ou
nombre impair de bits erronés dans le mot codé.

Le récepteur n'est pas pour autant en mesure de corriger systématiquement l'erreur. Il devra, pour bien faire, analyser toute l'information dont il dispose, c'est-à-dire l'ensemble des bits de parité, et en déduire un résultat aussi proche que possible du mot codé réel.

Supposons que les erreurs soient de probabilité égale sur tous les bits de $\overrightarrow{c}$ . La probabilité d'avoir j erreurs dans un bloc de taille n est

p(j, n) = 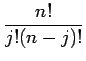$\displaystyle {\frac{{n!}}{{j!(n-j)!}}}$ p^j(1 - p)^n-j

(8.13)

où p représente la probabilité d'avoir un bit erroné. Dans le cas d'un bit de parité unique, la probabilité de ne pas détecter un bit erroné vaut donc

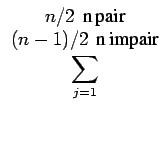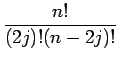$\displaystyle \sum_{{j=1}}^{{\begin{array}{c} n/2\,\textrm{ n}\,\textrm{pair}\\ (n-1)/2\textrm{ }\,\textrm{n}\,\textrm{impair}\end{array}}}$ $\displaystyle {\frac{{n!}}{{(2j)!(n-2j)!}}}$ p^2j(1 - p)^n-2j

(8.14)

La figure 8.4 montre la probabilité d'erreur P_e en fonction du rapport E_b/N₀ d'un démodulateur dont les messages ont été préalablement encodés par des codes (n, k).

**Figure 8.4:** Performance d'une détection PSK après codage.

La courbe (1, 1) représente la PSK à deux états (BPSK) sans encodage. Dans cet exemple, l'intérêt de l'encodage se manifeste au-delà d'une valeur de E_b/N₀ de 5, 5 [dB]. En-dessous de cette valeur, le codage introduit une perte de l'énergie E_b qui n'est pas compensée par une diminution de l'effet de bruit.