Table des matières of 8.6.1 Code de HAMMING

8.6.1 Code de HAMMING

Les codes de HAMMING constituent un sous-ensemble des codes en blocs pour lesquels (n, k) valent

(n, k) = (2^m -1, 2^m - 1 - m)

(8.37)

pour m = 2, 3,... Ces codes ont une distance minimale de 3. En conséquence, ils permettent la correction d'une erreur simple ou la détection de toute combinaison d'au plus deux erreurs.

SKLAR [21, page 298] montre que la probabilité d'erreur s'écrit

P_B $\displaystyle \simeq$ p - p(1 - p)^n-1

(8.38)

où p est la probabilité d'erreur du canal.

Il est utile de relier cette relation au taux d'erreur de détection classique. Prenons le cas d'une démodulation BPSK cohérente. Le taux d'erreur due à un bruit additif gaussien dans le canal est

P_e = $\displaystyle {\frac{{1}}{{2}}}$ $\displaystyle \left(\vphantom{\sqrt{\frac{E_{c}}{N_{0}}}}\right.$ $\displaystyle \sqrt{{\frac{E_{c}}{N_{0}}}}$ $\displaystyle \left.\vphantom{\sqrt{\frac{E_{c}}{N_{0}}}}\right)$

(8.39)

E_c représente l'énergie par symbole (binaire) du message source. On relie aisément l'énergie par bit réellement transmis E_b à E_c

E_b = $\displaystyle {\frac{{n}}{{k}}}$ E_c

(8.40)

Ce qui, dans le cas d'un code de HAMMING, conduit à déterminer la probabilité d'erreur par bit transmis sur base du changement de variable suivant

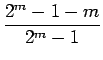$\displaystyle {\frac{{E_{c}}}{{N_{0}}}}$ = $\displaystyle {\frac{{2^{m}-1-m}}{{2^{m}-1}}}$ $\displaystyle {\frac{{E_{b}}}{{N_{0}}}}$

(8.41)

dans l'expression 8.39. Cette relation est utile si l'on veut comparer les performances d'un code comprenant ou non un précodage de redondance car elle permet de normaliser l'énergie par bit lors du tracé des courbes d'erreur. C'est ainsi qu'on calcule l'expression des courbes d'erreur correspondantes à différents couples de précodage.

Le code a pour effet de modifier l'inclinaison de la courbe de probabilité d'erreur. Au-delà d'une certaine valeur du rapport énergie par bit à puissance de bruit ( E_b/N₀), il est préférable. Au droit du point d'intersection d'une courbe de précodage avec la courbe sans précodage, un accroissement d'un dB signifie une différence de taux de probabilités d'erreur qui peut atteindre plusieurs ordres de grandeur.

Mais que l'on ne s'y trompe pas, l'utilisation d'un précodage n'a pas que des avantages. En effet, un taux de redondance de 1/2 entraîne le doublement de bande passante. Or, près de 0 [dB], l'absence de précodage garantit encore la meilleure performance. Utiliser un précodage dans cette plage conduirait à accroître la bande de fréquences tout en diminuant les performances.