Table des matières of 9.3.4 Modèle électrique

9.3.4 Modèle électrique

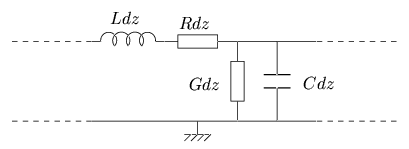
Après avoir déterminé les caractéristiques électriques principales d'une paire de conducteurs, on peut modéliser le fonctionnement électrique d'une ligne en imaginant le système comme une succession de bouts de lignes infinitésimaux; la figure 9.5 montre un bout de ligne infinitésimal.

**Figure 9.5:** Segment de ligne infinitésimal.

9.3.4.1 Paramètres primaires

R, L, C et G sont appelés paramètres primaires de la ligne avec:

R = résistance linéique élémentaire, représentant la résistance de la ligne par unité de longueur [ $\Omega$ /m]. Elle dépend en particulier de la section et de la nature du conducteur,
L = inductance linéique [H/m], modélisant la présence de champ électrique inter et intra-structures conductrices,
C = capacité linéique [F/m], caractérisant la capacité du diélectrique constituant la ligne,
G = admittance linéique [ $\Omega^{{-1}}_{}$ /m], représentant les pertes diélectriques et les défauts d'isolation de la ligne. Elle dépend de la nature des isolants.

9.3.4.2 Équations des télégraphistes

En mettant bout à bout des segments de ligne infinitésimaux et sur base du schéma de la figure 9.6, on obtient aisément le système d'équations suivantes, dites équations des télégraphistes,

$\displaystyle {\frac{{\partial V}}{{\partial z}}}$	=	RI + L $\displaystyle {\frac{{\partial I}}{{\partial t}}}$	(9.11)
$\displaystyle {\frac{{\partial I}}{{\partial z}}}$	=	GV + C $\displaystyle {\frac{{\partial V}}{{\partial t}}}$	(9.12)

**Figure 9.6:** Modèle d'une ligne de transmission électrique.

La solution du système s'écrit sous la forme d'une équation aux dérivées partielles du second ordre

$\displaystyle {\frac{{\partial^{2}V}}{{\partial z^{2}}}}$ = RGV + (RC + LG) $\displaystyle {\frac{{\partial V}}{{\partial t}}}$ + LC $\displaystyle {\frac{{\partial V^{2}}}{{\partial t^{2}}}}$

(9.13)

9.3.4.3 Cas particulier 1: ligne sans perte

Dans le cas d'une ligne sans perte (R = G = 0),

$\displaystyle {\frac{{\partial^{2}V}}{{\partial z^{2}}}}$ = LC $\displaystyle {\frac{{\partial V^{2}}}{{\partial t^{2}}}}$

(9.14)

ce qui correspond à une équation d'ondes bien connue dont une combinaison linéaire de signaux sinusoïdaux

V(z, t) = (A cos kz + B sin kz)(C cos 2 $\displaystyle \pi$ ft + D sin 2 $\displaystyle \pi$ ft)

(9.15)

9.3.4.4 Cas particulier 2: régime permanent

En régime permanent, V(z, t) = V(z)e^jt. La solution est de la forme

$\displaystyle {\frac{{\partial^{2}V}}{{\partial z^{2}}}}$ = (R + jL $\displaystyle \omega$ )(G + jC $\displaystyle \omega$ )V(z) = $\displaystyle \gamma^{{2}}_{}$ V(z)

(9.16)

En prenant $\gamma$ = $\alpha$ + j $\beta$ , on obtient

V(z) = V_ie^-z + V_re^z

(9.17)

L'onde est donc une onde atténuée par $\alpha$ . On voit tout de suite que l'atténuation croît avec la longueur de la ligne.

Ce facteur d'atténuation ne signifie pas que toute transmission soit impossible mais bien que le signal est atténué dès qu'il y a des pertes dans le conducteur. L'analyse en détail de la question montre que l'atténuation dépend de la fréquence. En fait, elle augmente avec la fréquence. Il est dès lors plus intéressant d'utiliser les basses fréquences pour la transmission. Néanmoins, rien n'empêche d'utiliser les zones d'atténuation plus importantes. C'est le mode de fonctionnement des modems à haut débit ADSL dont le spectre d'utilisation est montré à la figure 9.7.

**Figure 9.7:** Spectre d'un signal ADSL.

9.3.4.5 Paramètres secondaires

Les paramètres primaires ne modélisent la ligne que d'une manière grossière. On leur préfère souvent les paramètres dits secondaires suivants pour déterminer les propriétés du support :

impédance caractéristique Z_c
C'est une donnée complexe qui représente l'impédance d'entrée d'une ligne qui serait connectée à sa sortie sur une impédance égale à Z_c. En pratique, on doit absolument tenir compte de la valeur de l'impédance lors du raccordement de lignes ou d'équipements à un réseau. En effet, si deux lignes n'ont pas la même impédance, le droit du raccord est le lieu de réflexions parasites qui diminuent considérablement les performances de la transmission.
coefficient de propagation $\gamma$ (cf. supra)
Par définition : $\gamma$ = $\alpha$ + j $\beta$ où
- $\alpha$ = affaiblissement linéique en Néper/mètre [Np/m]^9.2
- $\beta$ = déphasage linéique (en [rad /m])

$\alpha$ représente les pertes subies par le signal électrique lors de la propagation le long de la ligne. Il se mesure en injectant un signal à l'une des extrémités de la ligne et en mesurant le signal reçu à l'autre extrémité. $\beta$ est lié à la longueur d'onde $\lambda$ et à la vitesse de propagation v de l'onde électromagnétique dans le support par

$\displaystyle \beta$ = $\displaystyle {\frac{{2\pi}}{{\lambda}}}$ = $\displaystyle {\frac{{2\pi f}}{{v}}}$

(9.18)

9.3.4.6 Relations entre les paramètres primaires et secondaires

Les paramètres primaires et secondaires sont liés par les relations suivantes

Z_c	=	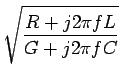$\displaystyle \sqrt{{\frac{R+j2\pi fL}{G+j2\pi fC}}}$	(9.19)
$\displaystyle \gamma$	=	$\displaystyle \sqrt{{(R+j2\pi fL)(G+j2\pi fC)}}$	(9.20)

Ces équations sont générales et valables sur tout type de ligne. Toutefois, certaines simplifications sont possibles en considérant un caractère plutôt inductif ou pas de ligne, une fréquence d'utilisation élevée ou non. D'autre part, on peut raisonnablement admettre que l'admittance linéique est négligeable, autrement dit G = 0, en raison de la présence d'un isolant entre les conducteurs.

Après étude des variations des paramètres secondaires en fonction de la fréquence pour une ligne à caractère inductif ou en haute fréquence ( 2 $\pi$ fL $\gg$ R), ou pour l'utilisation en fréquences vocales ( 2 $\pi$ fL $\ll$ R), on constate que :

si 2 $\pi$ fL $\ll$ R, Z_c est complexe et varie proportionnellement à 1/ $\sqrt{{f}}$ , $\alpha$ et $\beta$ à $\sqrt{{f}}$ , ceci provoquant des distorsions d'amplitude et de phase.
si 2 $\pi$ fL $\gg$ R, Z_c est réelle et indépendante de f, $\beta$ croît linéairement avec f ce qui se traduit par l'absence de distorsion de phase. $\alpha$ est indépendant de f s'il n'existe pas d'effet de peau (densité de courant uniforme dans toute la section du conducteur). Dans le cas contraire, une distorsion d'amplitude apparaît et $\alpha$ est proportionnel à $\sqrt{{f}}$ (ce qui est le cas des lignes en hautes fréquences).

9.3.4.7 Diaphonie

Lorsque deux lignes sont spatialement proches, il peut exister une influence parasite entre les signaux d'information qui sont véhiculés sur chaque voie. Cette perturbation est appelée diaphonie.

**Figure:** Paradiaphonie (NEXT) et télédiaphonie (FEXT).

Selon que la ligne perturbatrice provoque un parasite vers l'une ou l'autre des extrémités de la ligne parasitée, on parle de paradiaphonie (NEXT en anglais) ou de télédiaphonie (FEXT en anglais) (figure 9.8).

L'affaiblissement paradiaphonique est en particulier une grandeur importante dans la pratique pour caractériser un câble de transmission: il permet d'évaluer, à l'entrée d'une ligne perturbée, la perte de signal provoquée par la ligne perturbatrice voisine. Il dépend de la distance entre les lignes d'un même câble, des combinaisons des pas de torsades (pour les paires torsadées) et de la technique de construction du câble.

Notes

...^9.2: Le Néper est lié au décibel par la relation suivante: 1 [Np] = 8, 68 [dB].