|
Le son est une onde qui se propage dans l'air et qui est perceptible grâce au détecteur de pression qu'est le tympan, logé dans l'oreille. Ces vibrations sont ensuite converties en signaux transmis au cerveau par le nerf auditif.
Pour mieux saisir la notion de son, utilisons l'analogie avec la surface de l'eau. Jeter une pierre dans l'eau crée des ondulations de surface en forme de cercles concentriques. Ces ondes se propagent et, se heurtant aux berges, elles repartent en sens inverse. Le mécanisme de propagation du son est identique à ce phénomène où l'eau est remplacée par l'air et la pierre par une source sonore. Le son est le résultat d'une onde de pression qui voyage dans l'air, agite les molécules d'air et se réfléchit sur les obstacles qu'elle rencontre. Le tympan capte ces ondes qui sont in fine traduites en signaux électriques, comme le fait la membrane d'un micro.
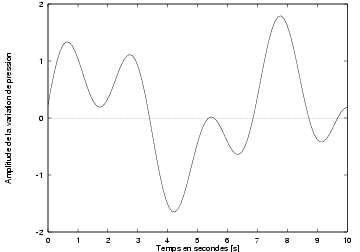
La figure 2.2 montre le relevé d'un son à l'oscilloscope. L'axe vertical représente l'écart d'une membrane (ou une mesure physique équivalente comme une tension électrique) par rapport à une position centrale en fonction du temps (axe horizontal).
Le son est une notion tellement complexe qu'il faut plusieurs paramètres pour le décrire. Le phénomène physique du son peut être étudié de manière quantitative et les propriétés de l'onde acoustique peuvent être exprimées sous la forme de grandeurs objectives. Nous allons en analyser quatre: hauteur tonale, intensité, timbre et durée. Ces quatre paramètres suffisent à décrire globalement un son. Pour permettre une description plus fine comme par exemple l'attaque d'un instrument, la norme audio MIDI définit près d'une quarantaine de paramètres supplémentaires.
La notion de ton est intimement liée à celle de fréquence.
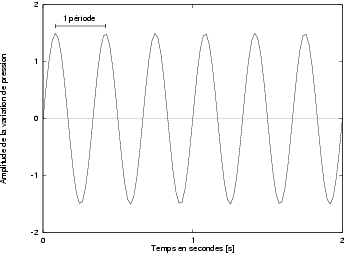
Une fréquence de 1000 [Hz] est donc une fréquence dont le cycle se reproduit 1000 fois par seconde. La figure 2.3 illustre ces notions.
|
La période est ainsi inversement proportionnelle à la fréquence (c'est-à-dire égale à 1/f): si la fréquence est de 3 [Hz], la période est de 1/3 seconde.
En principe, il n'y a pas de limitation dans la gamme des fréquences des sons possibles. Cependant notre oreille perçoit théoriquement des vibrations acoustiques allant de 20 [Hz] (son grave) à 20.000 [Hz] (son aigu). C'est la bande de fréquence qu'il faut restituer convenablement dans les systèmes haute fidélité, comme la radio FM, le canal son de la télévision ou le CD-audio. En radio AM cependant, on ne reproduit les fréquences que jusqu'à 4500 [Hz] et cela procure une qualité relativement bonne, même pour la musique. En téléphonie, où l'objectif est limité à l'intelligibilité du message, la bande de fréquence normalisée est 300 - 3400 [Hz]. Cette bande de fréquences est garantie de bout en bout du réseau. Un modem devra dont utiliser cette même gamme de fréquences pour permettre l'information numérique sous peine de perte d'information.
La limitation de la perception est importante pour tous les traitements liés au son; on part du principe qu'il est inutile d'enregistrer ou de stocker un son imperceptible. Nous reviendrons plus loin sur cette limitation et analyserons l'impact sur la phase de numérisation.
Les fréquences ont permis de définir les notes. Ainsi le do moyen qui se trouve au milieu du clavier d'un piano a une fréquence de 264 [Hz]. Un diapason produit le son la (pur) à 440 [Hz].
L'amplitude des variations de pression donne la seconde composante du son: l'intensité avec laquelle notre oreille percevra une note. L'intensité correspond au volume d'énergie d'une onde. L'amplitude du son est la mesure du changement de pression par rapport à une valeur moyenne. Cette mesure est l'intensité acoustique I qui est la puissance transportée par unité de surface du front d'onde et s'exprime, par exemple, en [W/cm2]. De telles grandeurs sont certes fort utiles, mais lorsqu'il s'agit de déterminer les conditions de bonne transmission de signaux sonores, il apparaît nécessaire de tenir compte des propriétés perceptives très particulières de l'ouïe. On fait alors appel à des grandeurs subjectives qui expriment ce que ressent l'être humain.
Un ensemble de fréquences et leurs variations d'intensité permettent d'avoir une sorte de carte d'identité du son, une forme d'onde générale, le timbre ou spectre. Il montre la proportion dans laquelle la fréquence fondamentale du son est mélangée à d'autres fréquences multiples de la fréquence fondamentale et appelées sons harmoniques. Un son qui n'est accompagné d'aucune harmonique est appelé son pur. Le timbre permet donc d'identifier la source sonore car chaque instrument produit un spectre de fréquences qui lui est propre.
Enfin, la répétition d'une onde sonore donne à son tour la durée du son. Elle s'exprime en secondes et correspond au temps pendant lequel l'énergie du son est perceptible. Sur le diagramme 2.3, la durée du son est de 2 secondes.
Avec ces quatre paramètres, on dispose d'une description suffisante
pour, par exemple, générer des sons. Produire de la musique de synthèse
implique que l'on passe de la simple notation des sons à leur transcription
dans la tonalité d'un instrument. Il faut pour cela prendre en compte
le timbre, toutes les harmoniques qui accompagnent la production d'un
son pur. L'analyse en fréquences et la transformée de FOURIER
sont le pivot de ces calculs et de tous les traitements effectués
sur les signaux sonores.
Le principe de l'analyse de FOURIER est celui du prisme: un rayon de lumière solaire pénétrant dans un prisme de cristal en ressort décomposé en plusieurs rayons. De même, le ``prisme mathématique de FOURIER'' décompose le son d'un instrument en ses harmoniques.
Prenons le cas d'un son continu produit par un instrument. Il est défini par une forme d'onde périodique, une fréquence qui se répète identiquement. Or notre oreille perçoit cette onde comme un assemblage de sons purs et non comme un son unitaire.
L'analyse spectrale classique consiste à déterminer mathématiquement de quelles harmoniques se compose une onde périodique. Par exemple, la vibration d'une corde de piano produit un signal complexe dans un diagramme de l'amplitude en fonction du temps. Analysée par la transformée de FOURIER, elle se décomposera en notes séparées.
Le principe est le suivant: tout signal périodique (ce qui est le cas du son) peut se décomposer en une série d'oscillations sinusoïdales2.1. Soit x(t) un signal sonore continu dans le temps t, la transformée de FOURIER de ce signal est définie comme suit:
Il s'agit d'une fonction dont la variable est la fréquence f. Un signal périodique est ainsi représenté par des raies, dont l'emplacement est fixé par la fréquence des oscillations observées dans le signal x(t), et l'amplitude par la valeur des coefficients définis par FOURIER.
Dans le sens inverse, connaissant le spectre X(f ) d'un signal, c'est-à-dire l'énergie de chacune des fréquences présentes dans le signal, on peut reconstituer sa forme initiale x(t) par la transformée de FOURIER inverse:
| x(t) = |
(2.2) |
Comme le signal X(f ) permet de reconstituer x(t), il y a équivalence entre les deux représentations, tout juste l'une est-elle une représentation temporelle et l'autre une représentation dans l'espace des fréquences. C'est toutefois la représentation fréquentielle qui est la plus utilisée. Ainsi, l'analyse de FOURIER sert de base pour l'analyse des sons et pour la création de signaux de synthèse.
Il existe trois grands modes de synthèse: la synthèse additive, la synthèse soustractive et la synthèse globale. La synthèse additive consiste à partir d'une fréquence et à compléter l'effet sonore par l'ajout de sons à d'autres fréquences. Contrairement à la synthèse additive, la synthèse soustractive débute par un signal riche et en soustrait les composantes. Son principe théorique revient à filtrer un signal pour ne garder que les composantes désirées.
La synthèse globale est une méthode qui repose sur des relations mathématiques abstraites. Une technique importante est la modulation de fréquences, par ailleurs utilisée par les ondes radio FM.
Comme nous l'avons signalé, tous les sons ne sont pas perceptibles. De plus, en raison de limitations physiques, certains équipements s'avèrent incapables de traiter certaines fréquences. On parle alors de bande passante.