A.1.3 Exemples

  1. Considérons un signal rectangulaire g(t) de durée T et d'amplitude A. Afin de définir mathématiquement ce signal, nous introduisons la fonction

    rect(t) = Rect[-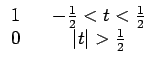$\scriptstyle {\frac{{1}}{{2}}}$,$\scriptstyle {\frac{{1}}{{2}}}$](t) = $\displaystyle \left\{\vphantom{ \begin{array}{ccc} 1 & & -\frac{1}{2}<t<\frac{1}{2}\\ 0 & & \left\vert t\right\vert>\frac{1}{2}\end{array}}\right.$$\displaystyle \begin{array}{ccc} 1 & & -\frac{1}{2}<t<\frac{1}{2}\\ 0 & & \left\vert t\right\vert>\frac{1}{2}\end{array}$ (A.20)

    appelée en général fonction rectangle. Dès lors, nous pouvons écrire

    g(t) = A rect$\displaystyle \left(\vphantom{\frac{t}{T}}\right.$$\displaystyle {\frac{{t}}{{T}}}$$\displaystyle \left.\vphantom{\frac{t}{T}}\right)$ = A Rect[-$\scriptstyle {\frac{{T}}{{2}}}$,$\scriptstyle {\frac{{T}}{{2}}}$](t) (A.21)

    La transformée de FOURIER du signal g(t) est donnée par
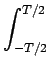    $\displaystyle \mathcal {G}$(f ) = $\displaystyle \int_{{-T/2}}^{{T/2}}$A e-2$\scriptstyle \pi$jftdt (A.22)
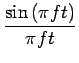      = AT$\displaystyle \left(\vphantom{\frac{\sin\left(\pi ft\right)}{\pi ft}}\right.$$\displaystyle {\frac{{\sin\left(\pi ft\right)}}{{\pi ft}}}$$\displaystyle \left.\vphantom{\frac{\sin\left(\pi ft\right)}{\pi ft}}\right)$ (A.23)

    Afin de simplifier la notation précédente, nous introduisons la fonction sinus cardinal, sinc, définie par

    sinc(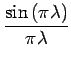$\displaystyle \lambda$) = $\displaystyle {\frac{{\sin\left(\pi\lambda\right)}}{{\pi\lambda}}}$ (A.24)

    Finalement, il vient

    $\displaystyle \mathcal {G}$(f )= AT sinc(fT) (A.25)

    Nous avons donc la paire de transformées de FOURIER:

    A rect$\displaystyle \left(\vphantom{\frac{t}{T}}\right.$$\displaystyle {\frac{{t}}{{T}}}$$\displaystyle \left.\vphantom{\frac{t}{T}}\right)$ $\displaystyle \rightleftharpoons$ AT sinc(ft) (A.26)

  2. Considérons le signal g(t) suivant:

    g(t) = A sinc(2Wt) (A.27)

    En appliquant la propriété de dualité de la transformée de FOURIER à la relation A.26 et étant donné que la fonction rectangle est une fonction paire du temps, il vient

    AT sinc(Tt) $\displaystyle \rightleftharpoons$ A rect$\displaystyle \left(\vphantom{\frac{f}{T}}\right.$$\displaystyle {\frac{{f}}{{T}}}$$\displaystyle \left.\vphantom{\frac{f}{T}}\right)$ (A.28)

    En posant T = 2W, nous obtenons la paire de transformées de FOURIER suivante

    A sinc(2Wt) $\displaystyle \rightleftharpoons$ $\displaystyle {\frac{{A}}{{2W}}}$rect$\displaystyle \left(\vphantom{\frac{f}{2W}}\right.$$\displaystyle {\frac{{f}}{{2W}}}$$\displaystyle \left.\vphantom{\frac{f}{2W}}\right)$ (A.29)

Marc Van Droogenbroeck. Tous droits réservés.
2004-06-11