Table des matières of 3.1.1 Représentation des signaux

3.1.1 Représentation des signaux

Pour l'étude de systèmes de communication, on peut distinguer plusieurs classes de signaux. Ces classes établissent les distinctions suivantes entre signaux, détaillées plus loin:

analogiques ou numériques,
périodiques ou apériodiques,
déterministes ou stochastiques,
d'énergie ou de puissance.

3.1.1.1 Signaux analogiques ou numériques

Un signal x(t) analogique est une fonction continue pour tout temps t. Un signal numérique est un signal temporel discontinu; on le notera x[n] où n est l'indice d'un élément pris dans l'ensemble d'instants {t₀, t₁,...}. On parle encore de signaux à temps discret.

3.1.1.2 Signaux périodiques ou apériodiques

Un signal x(t) est périodique s'il satisfait la relation suivante

x(t) = x(t + T₀) $\displaystyle \forall$ t

(3.1)

où t est la variable de temps et T₀ une constante. La plus petite valeur T₀ pour laquelle cette relation est vérifiée est appelée période fondamentale de x(t). Un intervalle de temps d'une durée T₀ couvre donc un cycle complet du signal x(t). S'il n'existe pas de constante pour laquelle la relation 3.1 est respectée, on dit que le signal x(t) est apériodique ou non-périodique.

3.1.1.3 Signaux déterministes ou stochastiques

Un signal déterministe a une évolution connue et prévisible, contrairement aux signaux aléatoires ou stochastiques. Si un signal source est en grande partie déterministe à l'émetteur, le bruit qui l'affecte durant la transmission est inconnu. Le tableau 3.1 reprend les caractéristiques des signaux à l'émetteur et au récepteur.

Tableau 3.1: Nature des signaux dans une chaîne de télécommunications.

	Émetteur	Récepteur
Signal utile	déterministe	aléatoire
Bruit et interférences	aléatoire	aléatoire

Au vu de la nature des signaux, l'analyse des systèmes de télécommunications nécessitera le recours à des outils stochastiques au moment d'établir les performances. Il en va de même pour l'utilisation de signaux numériques pour lesquels les performances s'exprimeront par des probabilités d'erreur durant la transmission.

3.1.1.4 Signaux d'énergie ou de puissance

Tout au long de la chaîne de télécommunications, on traite des signaux électriques caractérisés par une tension ou un courant. Soit une tension v(t) qui, à travers une résistance R, produit un courant i(t). La puissance instantanée dissipée dans cette résistance est définie par

p(t) = 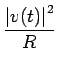$\displaystyle {\frac{{\left\vert v(t)\right\vert^{2}}}{{R}}}$

(3.2)

ou encore

p(t) = R $\displaystyle \left\vert\vphantom{i(t)}\right.$ i(t) $\displaystyle \left.\vphantom{i(t)}\right\vert^{{2}}_{}$

(3.3)

Quelle qu'en soit l'expression, la puissance instantanée est une fonction quadratique du signal caractéristique. À travers une charge unitaire de 1 Ohm, noté [ $\Omega$ ], les expressions sont même égales si bien qu'en définitive, il est de coutume de normaliser l'expression pour une résistance de 1 [ $\Omega$ ]. Pour un signal de tension ou de courant, on obtient alors

Définition 13 [Puissance instantanée normalisée]

p(t) = $\displaystyle \left\vert\vphantom{x(t)}\right.$ x(t) $\displaystyle \left.\vphantom{x(t)}\right\vert^{{2}}_{}$

(3.4)

Définition 14 [Énergie] Sur base de cette convention, l'énergie totale du signal x(t) est définie par

E	=	$\displaystyle \lim_{{T\rightarrow+\infty}}^{}$ $\displaystyle \int_{{-T}}^{{T}}$ $\displaystyle \left\vert\vphantom{x(t)}\right.$ x(t) $\displaystyle \left.\vphantom{x(t)}\right\vert^{{2}}_{}$ dt	(3.5)
	=	$\displaystyle \int_{{-\infty}}^{{+\infty}}$ $\displaystyle \left\vert\vphantom{x(t)}\right.$ x(t) $\displaystyle \left.\vphantom{x(t)}\right\vert^{{2}}_{}$ dt	(3.6)

Certains signaux possède une énergie infinie. On utilise alors la notion de puissance moyenne qui est la moyenne temporelle de l'énergie.

Définition 15 [Puissance moyenne d'un signal] Il en découle une puissance moyenne du signal x(t) s'exprimant

P = $\displaystyle \lim_{{T\rightarrow+\infty}}^{}$ $\displaystyle {\frac{{1}}{{2T}}}$ $\displaystyle \int_{{-T}}^{{+T}}$ $\displaystyle \left\vert\vphantom{x(t)}\right.$ x(t) $\displaystyle \left.\vphantom{x(t)}\right\vert^{{2}}_{}$ dt

(3.7)

Dans le cas d'un signal périodique de période T₀, l'expression de la puissance moyenne devient

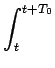P = $\displaystyle {\frac{{1}}{{T_{0}}}}$ $\displaystyle \int_{{t}}^{{t+T_{0}}}$ $\displaystyle \left\vert\vphantom{x(t)}\right.$ x(t) $\displaystyle \left.\vphantom{x(t)}\right\vert^{{2}}_{}$ dt

(3.8)

Les définitions d'énergie et de puissance amènent à distinguer deux types de signaux:

les signaux à énergie finie, pour lesquels 0 < E < + $\infty$ . Un signal physiquement réalisable est à énergie finie.
les signaux à puissance finie. Dans ce cas, la puissance moyenne est bornée, à savoir 0 < P < + $\infty$ .

Ces deux contraintes sont mutuellement exclusives. En particulier, un signal à énergie finie a une puissance moyenne nulle alors qu'un signal à puissance finie possède une énergie infinie.

Les signaux déterministes et apériodiques sont à énergie finie alors que les signaux périodiques ou aléatoires ont généralement une puissance finie non nulle. Signalons qu'il s'agit de modélisation et qu'en conséquence, certains signaux n'ont pas de réelle signification physique pour des temps infinis, ce qui n'empêche pas qu'ils puissent être d'une grande aide!

3.1.1.5 Décibel

Pour les calculs de puissance, on utilise fréquemment une unité basée sur le logarithme. Cette unité est le décibel, noté dB. L'introduction de la notion de décibel est destinée à pouvoir décrire un signal de puissance en termes de décades, car les niveaux de puissance tout au long d'une chaîne de transmission varient dans des proportions considérables; c'est donc un changement d'échelle.

Pour un signal d'énergie ou de puissance x, la relation entre unité décimale et décibel est la suivante

x $\displaystyle \leftrightarrow$ 10 log₁₀(x)

(3.9)

L'usage des décibels peut aussi s'exprimer relativement à une puissance de référence. C'est ainsi qu'on définit le dBW et le dBm ^3.1 comme l'écart par rapport à, respectivement, 1 [W] et 1 [mW]. La puissance P vaut, en dBm,

P [dBm] = 10 log₁₀ $\displaystyle {\frac{{P\,[mW]}}{{1\,[mW]}}}$

(3.10)

Le tableau 3.2 reprend quelques valeurs essentielles.

Tableau 3.2: Valeurs de puissance exprimées en décibels (dBW).

x [W]	10 log₁₀(x) [dBW]
1 [W]	0 [dBW]
2 [W]	3 [dBW]
0, 5 [W]	-3 [dBW]
5 [W]	7 [dBW]
10ⁿ [W]	10n [dBW]

Un calcul simple montre que 50 [W] équivaut à 17 [dBW] ou à 47 [dBm].

Pour le calcul de transmission radio, on parle d'intensité de champ électrique en [dB $\mu$ V/m]. Or, le volt ne représente pas une mesure de puissance, contrairement à l'unité du volt au carré. En définitive, pour une tension U exprimée en [V], les décibels s'expriment par

10 log₁₀ $\displaystyle \left(\vphantom{\frac{U}{1\,[V]}}\right.$ $\displaystyle {\frac{{U}}{{1\,[V]}}}$ $\displaystyle \left.\vphantom{\frac{U}{1\,[V]}}\right)^{{2}}_{}$ = 20 log₁₀ $\displaystyle {\frac{{U}}{{1\,[V]}}}$

(3.11)

En conclusion, pour des grandeurs dont le carré représente une puissance,

x $\displaystyle \leftrightarrow$ 20 log₁₀(x)

(3.12)

On notera la présence d'un facteur 20 au lieu de 10 comme pour les puissances.

Exemple. Le confort d'écoute en radiodiffusion FM stéréo est défini par un seuil inférieur valant 1 [mV/m]. En [dB $\mu$ V/m], ce seuil s'exprime comme suit

20 log₁₀ $\displaystyle {\frac{{1\,[mV/m]}}{{1\,[\mu V/m]}}}$ = 20 log₁₀ $\displaystyle {\frac{{1000\,[\mu V/m]}}{{1\,[\mu V/m]}}}$ = 60 [dB $\displaystyle \mu$ V/m]

(3.13)

3.1.1.6 Rapport signal à bruit

Le rapport de la puissance du signal utile à celle du bruit, notées respectivement P_S et P_N, permet souvent de qualifier la qualité de la transmission.

Définition 16 [Rapport signal à bruit ou Signal to Noise Ratio (SNR)] Le rapport signal à bruit, exprimé en décibel, vaut le quotient de puissance suivant

$\displaystyle \left(\vphantom{\frac{S}{N}}\right.$ $\displaystyle {\frac{{S}}{{N}}}$ $\displaystyle \left.\vphantom{\frac{S}{N}}\right)$ = 10 log₁₀ $\displaystyle \left(\vphantom{\frac{P_{s}}{P_{N}}}\right.$ $\displaystyle {\frac{{P_{s}}}{{P_{N}}}}$ $\displaystyle \left.\vphantom{\frac{P_{s}}{P_{N}}}\right)$ [dB]

(3.14)

Il s'agit d'un critère abondamment utilisé pour la description des performances d'un système.

Notes

... ^3.1: En toute rigueur, on devrait noter dBmW.