Table des matières of 3.2.4 Système de transmission idéal

3.2.4 Système de transmission idéal

Soit un signal à transmettre x(t). Comme l'information réside habituellement dans la forme de ce signal, on admet que l'information n'est pas affectée si, au cours de la transmission, le signal ne subit, à travers le canal, que l'effet d'une multiplication de l'amplitude par une constante (amplification ou atténuation) ou l'effet d'un retard de transmission raisonnable. Ainsi, lors d'une communication téléphonique, le signal subira des amplifications et un retard de l'ordre de la dizaine de milli-secondes.

Définition 19 [Système de transmission idéal] Si le signal porteur d'information est représenté à l'entrée par une fonction x(t), le système de transmission peut être considéré comme idéal s'il fournit en sortie un signal donné par Kx(t - $\tau$ ).

Dans ce cas, K est un facteur d'amplification ou d'atténuation de l'amplitude et $\tau$ est un retard; ces deux grandeurs peuvent prendre des valeurs arbitraires mais raisonnables pour l'application considérée. L'information étant, par nature, imprévisible, ce comportement doit être valable non seulement pour le signal x(t) mais aussi pour toute la classe des fonctions représentant les signaux possibles. La conclusion est immédiate: le système de transmission idéal doit être linéaire, permanent et posséder une transmittance de la forme

$\displaystyle \mathcal {H}$ (f )= Ke^-2jf

(3.26)

On a donc la double condition suivante, outre que le système doit être linéaire et permanent:

Le module de la transmittance doit être constant.
Le déphasage doit être proportionnel à la fréquence, le coefficient (négatif) de proportionnalité étant le retard.

Il est clair que ces conditions ne doivent être satisfaites que sur la bande de fréquences occupée par l'ensemble des signaux possibles.

**Figure 3.2:** Transmittance d'un système idéal.

3.2.4.1 Distorsions de linéarité

Si, le système de transmission étant linéaire et permanent, l'une ou l'autre des deux conditions précédentes n'est pas remplie, le signal est affecté d'une distorsion. Ces deux types de distorsion sont dites linéaires.

On peut donner de ces types de distorsion une interprétation mathématique. Si le module de la transmittance $\mathcal {H}$ (f ) n'est pas constant, cela signifie que les différentes composantes du signal d'entrée sont transmises avec un coefficient d'amplification ou d'atténuation différents.

Si le déphasage

$\displaystyle \phi$ (f )= arg $\displaystyle \mathcal {H}$ (f )

(3.27)

n'est pas proportionnel à la fréquence, cela signifie que les différentes composantes spectrales ont des temps de propagation inégaux à travers le système et arrivent donc en ordre dispersé; c'est pourquoi un système présentant de la distorsion de phase est dit dispersif.

3.2.4.1.1 Délai de groupe et de phase.

Il est commode d'identifier la distorsion de phase d'un système linéaire par la dérivée de la phase. Plus précisément, on utilise la grandeur suivante

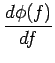$\displaystyle \tau_{{g}}^{}$ = - $\displaystyle {\frac{{1}}{{2\pi}}}$ $\displaystyle {\frac{{d\phi(f)}}{{df}}}$

(3.28)

appelée délai de groupe. Pour un système idéal,

$\displaystyle \phi$ (f )= - 2 $\displaystyle \pi$ f $\displaystyle \tau_{{0}}^{}$

(3.29)

ce qui fournit un délai de groupe

$\displaystyle \tau_{{g}}^{}$	=	- $\displaystyle {\frac{{1}}{{2\pi}}}$ (- 2 $\displaystyle \pi$ $\displaystyle \tau_{{0}}^{}$ )	(3.30)
	=	$\displaystyle \tau_{{0}}^{}$	(3.31)

Le délai de groupe est donc constant pour un système idéal.

Deux composantes fréquentielles d'un groupe de fréquences subissent un délai fourni par $\tau_{{g}}^{}$ . Un système à l'entrée duquel on injecte un signal mono-fréquentiel est toujours idéal. Le délai de cette composante unique, appelée délai de phase, vaut

$\displaystyle \tau_{{p}}^{}$ = - $\displaystyle {\frac{{\phi(f)}}{{2\pi f}}}$

(3.32)

Dans le cas d'un système idéal,

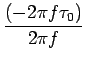$\displaystyle \tau_{{p}}^{}$ = - $\displaystyle {\frac{{(-2\pi f\tau_{0})}}{{2\pi f}}}$ = $\displaystyle \tau_{{0}}^{}$

(3.33)

Autrement dit, les délais de groupe et de phase d'un tel système sont égaux.

3.2.4.2 Distorsions non linéaires

L'étude de systèmes non linéaires n'est guère aisée par manque d'outil adéquat. Nous l'aborderons par le biais d'un exemple. Considérons un système qui, à tout signal d'entrée x(t), associe la sortie y(t) suivante

y(t) = ax(t) + bx²(t)

(3.34)

Soit le signal d'entrée suivant

x(t) = A₀cos(2 $\displaystyle \pi$ f₀t) + A₁cos(2 $\displaystyle \pi$ f₁t)

(3.35)

La sortie vaut

y(t)	=	aA₀cos(2 $\displaystyle \pi$ f₀t) + aA₁cos(2 $\displaystyle \pi$ f₁t)
	+	bA₀²cos²(2 $\displaystyle \pi$ f₀t) + bA₁²cos²(2 $\displaystyle \pi$ f₁t)
	+	2bA₀A₁cos(2 $\displaystyle \pi$ f₀t)cos(2 $\displaystyle \pi$ f₁t)	(3.36)
	=	aA₀cos(2 $\displaystyle \pi$ f₀t) + aA₁cos(2 $\displaystyle \pi$ f₁t)
	+	$\displaystyle {\frac{{bA_{0}^{2}}}{{2}}}$ $\displaystyle \left(\vphantom{1+\cos(4\pi f_{0}t)}\right.$ 1 + cos(4 $\displaystyle \pi$ f₀t) $\displaystyle \left.\vphantom{1+\cos(4\pi f_{0}t)}\right)$ + $\displaystyle {\frac{{bA_{1}^{2}}}{{2}}}$ $\displaystyle \left(\vphantom{1+\cos(4\pi f_{1}t)}\right.$ 1 + cos(4 $\displaystyle \pi$ f₁t) $\displaystyle \left.\vphantom{1+\cos(4\pi f_{1}t)}\right)$
	+	bA₀A₁ $\displaystyle \left(\vphantom{\cos(2\pi(f_{0}+f_{1})t)+\cos(2\pi(f_{0}-f_{1})t)}\right.$ cos(2 $\displaystyle \pi$ (f₀ + f₁)t) + cos(2 $\displaystyle \pi$ (f₀ - f₁)t) $\displaystyle \left.\vphantom{\cos(2\pi(f_{0}+f_{1})t)+\cos(2\pi(f_{0}-f_{1})t)}\right)$	(3.37)

La non linéarité se traduit par la présence en sortie de fréquences nouvelles. Ces signaux introduisent une distorsion harmonique, appelée intermodulation. C'est une règle générale de retrouver les fréquences doubles pour une relation entrée-sortie en x²(t), les fréquences tripes pour x³(t), etc.

En pratique, les non linéarités sont très fréquentes; l'utilisation de circuits actifs tels que des amplificateurs ou répéteurs, ayant des gains non linéaires ou pouvant saturer, entraîne des non linéarités. Ces distorsions sont difficilement modélisées et compensées mais, fort heureusement, elles constituent généralement un phénomène de faible ampleur.