4.2.3 Entropie d'une source

Considérons une source discrète sans mémoire, notée S. Supposons que cette source corresponde à un alphabet de n symboles différents, appelé alphabet de source :

A₁, A₂, ..., A_n (4.8)

À chacun de ces symboles, on associe une probabilité d'émission

p(A₁), p(A₂), ..., p(A_n) (4.9)

avec la contrainte

$$\sum_{{i=1}}^{{n}}$$ (4.10)

La connaissance de la probabilité d'émission de chaque symbole de la source permet de déduire l'information propre associée à chaque symbole :

-log₂p(A₁),  - log₂p(A₂), ...,  - log₂p(A_n) (4.11)

Définition 22   L'entropie de la source est alors définie par

$$\sum_{{i=1}}^{{n}}$$ (4.12)

Cette grandeur représente l'information moyenne par symbole (ou incertitude moyenne par symbole). En base 2, l'entropie s'exprime en bit par symbole. Plus l'entropie de la source est grande, plus il y a d'incertitude et donc d'information liée à la source. Dans cette définition, il est supposé que tous les symboles ont une probabilité d'émission non nulle. On montre que l'entropie est maximale et vaut log₂n lorsque tous ses symboles sont équiprobables. En effet, prenons le cas d'une source binaire comprenant les deux symboles A₁ et A₂, telle que

$$\left\{\vphantom{ \begin{array}{c} p(A_{1})=k\\ p(A_{2})=1-k\end{array}}\right.$$$$\begin{array}{c} p(A_{1})=k\\ p(A_{2})=1-k\end{array}$$

où k $\in$ $\left[\vphantom{0,1}\right.$0, 1$\left.\vphantom{0,1}\right]$. L'entropie de cette source vaut, par définition,

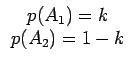
H(S) = - k log₂k - (1 - k)log₂(1 - k) (4.13)

L'entropie est une fonction de la probabilité k. Notons, par soucis de clarté, la valeur de l'entropie de source comme une fonction de son argument H(k). Cette fonction est représentée à la figure 4.2.

Figure 4.2: Entropie d'une source binaire en fonction de la probabilité de ses symboles.

 

On peut tout d'abord remarquer que l'entropie est nulle pour k = 1 (le symbole A₁ est émis avec certitude) et pour k = 0 (le symbole A₂ est émis avec certitude), ce qui correspond au cas où il n'y a aucune incertitude sur le symbole émis par la source. De plus, l'entropie atteint son maximum pour k = 0, 5 -la source a alors une entropie d'information de 1 [b/symbole]- , ce qui correspond au fait que les deux symboles sont équiprobables. En d'autres mots, il est tout aussi probable que la source émette le symbole A₁ que le symbole A₂.

Le raisonnement précédent est aisément généralisé au cas d'une source à n symboles équiprobables: p(A₁) = p(A₂) = ... = p(A_n) = 1/n , et l'entropie maximale de la source vaut alors

$$\sum_{{i=1}}^{{n}} {\frac{{1}}{{n}}} {\frac{{1}}{{n}}}$$ H_max(S) = (4.14)

$${\frac{{1}}{{n}}} {\frac{{1}}{{n}}} \sum_{{i=1}}^{{n}}$$ = (4.15)

= log₂n (4.16)

Une source de 8 symboles équiprobables génèrent donc des symboles dont en moyenne 3 bits d'information par symboles. Ce résultat est intuitivement satisfaisant car, de fait, il faut au plus 3 bits pour représenter toutes les valeurs de la source.

L'entropie d'une source représente donc l'incertitude liée à cette source. Plus il est difficile de prédire le symbole émis par une source, plus grande est son entropie.