|
Le principe de la méthode de HUFFMAN est d'associer aux symboles les plus probables le plus petit nombre de bits et aux symboles les moins probables le plus grand nombre de bits.
La première étape de la méthode consiste à réorganiser les symboles par ordre de probabilité décroissante. Chaque symbole est alors associé à une feuille d'un arbre en construction. On relie ensuite les feuilles en créant un noeud auquel on associe la somme des probabilités des deux symboles correspondants. À chaque étape, on fusionne les 2 noeuds (ou feuilles) ayant les probabilités les plus faibles. On répète ce processus jusqu'à ce qu'il ne reste plus qu'un seul noeud dont la probabilité associée vaut 1.
Exemple. Considérons une source à 4 symboles
A1, A2, A3, A4
respectivement de probabilité
p(A1) = 0, 5, p(A2) = 0, 25, P(A3) = 0, 125, p(A4) = 0, 125.
Dans cet exemple, les symboles ont déjà été réorganisés par ordre
décroissant de leur probabilité respective. L'arbre est construit
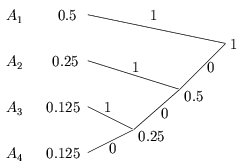
comme indiqué à la figure 4.3.
Une fois l'arbre construit, on associe à chaque branche de l'arbre
un symbole 0 ou 1. Il suffit de redescendre l'arbre jusqu'aux
symboles pour déterminer le code correspondant
| A1 | 1 | ||
| A2 | 01 | ||
| A3 | 001 | ||
| A4 | 000 |
Appelons l (Ai) le nombre de bits associé au symbole Ai.
Dès lors, nous avons
| l (A1) | = | 1 | |
| l (A2) | = | 2 | |
| l (A3) | = | 3 | |
| l (A4) | = | 3 |
Le nombre moyen de bits utilisés par symbole, M, est donné par
| M = |
(4.20) |
| H(S) = - |
(4.21) |
Il vient donc que le code obtenu par la méthode de HUFFMAN est optimal. Il faut remarquer que l'association triviale (A1 = 00, A2 = 01, A3 = 10, A4 = 11) aurait fourni un code de 2 bits par symboles. L'exemple précédent pourrait faire croire que le code de HUFFMAN conduit toujours à M = H(S). Ce n'est certes pas le cas et, de plus, la solution n'est pas nécessaire unique. Ainsi, dans l'exemple précédent, on peut permuter les mots de code de A3 et A4 sans affecter la valeur de M.