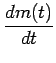Sous-sections
Dans la modulation angulaire, le signal modulé prend la forme
s(t) = Accos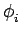 (t) (t) |
(5.29) |
où
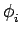 (t), appelée phase instantanée du signal
modulé, est une fonction du signal modulant. En l'absence de modulation,
on aurait évidemment
(t), appelée phase instantanée du signal
modulé, est une fonction du signal modulant. En l'absence de modulation,
on aurait évidemment
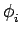 (t) = 2
(t) = 2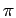 fct +
fct + 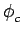 où
où 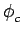 est la phase au temps t = 0. Remarquons que la modulation angulaire
n'affecte pas l'amplitude la porteuse.
est la phase au temps t = 0. Remarquons que la modulation angulaire
n'affecte pas l'amplitude la porteuse.
Définition 31
L'amplitude de la déviation instantanée de phase
est appelée indice de modulation.
Elle joue un rôle important, comme nous le verrons ultérieurement.
La déviation instantanée de phase peut être interprétée comme une
variation de la fréquence.
Définition 32
Par définition, la quantité
fi(t) = 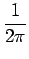  |
(5.32) |
est la fréquence instantanée.
Bien entendu, en l'absence de modulation angulaire, on retrouve la
fréquence de la porteuse fc. Ce n'est pas tant la fréquence
qui importe mais la différence entre la fréquence instantanée et la
fréquence porteuse. Tout comme pour la phase, on définit la déviation
instantanée de fréquence.
Définition 33
La déviation instantanée de fréquence
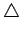 fi(t) est l'écart
entre la fréquence de la porteuse et la fréquence instantanée
fi(t) est l'écart
entre la fréquence de la porteuse et la fréquence instantanée
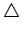 fi(t) = fi(t) - fc fi(t) = fi(t) - fc |
(5.33) |
Définition 34
Le maximum de la déviation instantanée de fréquence
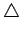 fi(t)
fournit l'excursion de fréquence
fi(t)
fournit l'excursion de fréquence
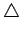 f définie par
f définie par
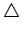 f = max| f = max|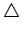 fi(t)| fi(t)| |
(5.34) |
Des définitions précises des divers types de modulation angulaire
seront données plus loin. On peut déjà dire que la modulation angulaire
consiste à faire varier, selon une loi linéaire bien précise, une
des quantités
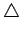
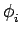 (t) ou
(t) ou
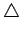 fi(t). Comme
suite des définitions qui précèdent, il apparaît que l'on ne peut
faire varier l'une sans l'autre; une modulation de phase entraîne
donc une modulation de fréquence et inversement.
fi(t). Comme
suite des définitions qui précèdent, il apparaît que l'on ne peut
faire varier l'une sans l'autre; une modulation de phase entraîne
donc une modulation de fréquence et inversement.
Dans le jargon technique, on utilise aussi le terme de taux
de modulation:
il s'agit de la quantité
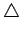 f /
f /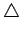 fmax, où
fmax, où
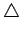 fmax
est la valeur maximale de l'excursion de fréquence autorisée par les
règlements régissant le partage des fréquences, par exemple par le
Règlement des radiocommunications. Ainsi, en radiodiffusion sonore
à modulation de fréquence, on impose
fmax
est la valeur maximale de l'excursion de fréquence autorisée par les
règlements régissant le partage des fréquences, par exemple par le
Règlement des radiocommunications. Ainsi, en radiodiffusion sonore
à modulation de fréquence, on impose
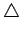 fmax = 75 [kHz].
fmax = 75 [kHz].
À condition de faire varier un paramètre de la phase comme une fonction
linéaire du signal modulant, on obtient une modulation appelée modulation
angulaire. Dans cette modulation, le signal modulant m(t) est
généralement un signal alternatif, tel qu'un signal sonore, oscillant
entre -1 et +1. Pour l'instant, il s'agira d'un signal continu,
auquel cas on parle de modulation angulaire analogique de type
F3.
Parmi toutes les possibilités de modulation angulaire, on distingue
la modulation de phase pure et la modulation de fréquence pure.
Définition 35
La modulation de phase (Phase Modulation,
PM) consiste à faire varier la phase
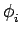 (t) en
fonction du signal modulant5.3 m(t), à savoir (on prend
(t) en
fonction du signal modulant5.3 m(t), à savoir (on prend
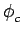 = 0)
= 0)
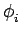 (t) = 2 (t) = 2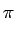 fct + kpm(t) fct + kpm(t) |
(5.35) |
Le terme
2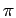 fct représente la phase de la porteuse en l'absence
de modulation. La présence d'une tension modulante affecte cette phase
en fonction d'un coefficient kp qui représente la sensibilité
du modulateur; elle s'exprime en radians par volt. Le signal modulé
vaut donc
fct représente la phase de la porteuse en l'absence
de modulation. La présence d'une tension modulante affecte cette phase
en fonction d'un coefficient kp qui représente la sensibilité
du modulateur; elle s'exprime en radians par volt. Le signal modulé
vaut donc
s(t) = Accos(2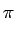 fct + kpm(t)) fct + kpm(t)) |
(5.36) |
La fréquence instantanée de la cosinusoïde est la dérivée de la phase
divisée par 2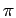
Il s'ensuit que la modulation de phase revient à modifier la fréquence
de la porteuse. La déviation de fréquence instantanée vaut
Définition 36
Par définition de la modulation de fréquence (Frequency Modulation,
FM), la déviation instantanée fi(t) est proportionnelle
au signal modulant
| fi(t) = fc + kfm(t) |
(5.39) |
La fréquence résultante est donc liée, via la sensibilité du modulateur
kf exprimée en [Hz/V], au signal modulant. La phase du
signal modulé se calcule par l'intégrale de la fréquence instantanée
(on prend
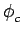 = 0)
= 0)
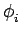 (t) = 2 (t) = 2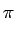 fct + 2 fct + 2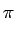 kf kf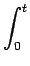 m(t')dt' m(t')dt' |
(5.40) |
Dès lors le signal modulé vaut
s(t) = Accos(2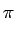 fct + 2 fct + 2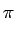 kf kf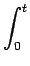 m(t')dt') m(t')dt') |
(5.41) |
Les relations 5.37 et 5.40
mettent bien en évidence qu'une modulation de phase entraîne une modulation
de fréquence, et vice versa. Plus précisément, on peut affirmer que
la modulation de phase se réduit à une modulation de fréquence par
le signal modulant préalablement dérivé. Inversement, une modulation
de fréquence est une modulation de phase par l'intégrale du signal
modulant. Ces schémas sont représentés à la figure 5.10.
Figure 5.10:
Liens entre modulation de phase et modulation de fréquence.
|
|
En conséquence de la modulation de la phase, les passages par 0
de la fonction ne sont plus équidistants; par contre, l'enveloppe
reste constante. La figure 5.11 montre un signal
modulant original et les signaux modulés respectivement en amplitude,
en phase et en fréquence.
Figure 5.11:
Signal modulant et signaux modulés respectivement en AM, PM et FM.
|
|
Notes
- ... modulant5.3
- Nous n'exigeons plus que le signal modulant m(t) soit inférieur
à 1 en modulation angulaire.
Marc Van Droogenbroeck. Tous droits réservés.
2004-06-11
![]() (t), appelée phase instantanée du signal
modulé, est une fonction du signal modulant. En l'absence de modulation,
on aurait évidemment
(t), appelée phase instantanée du signal
modulé, est une fonction du signal modulant. En l'absence de modulation,
on aurait évidemment
![]() (t) = 2
(t) = 2![]() fct +
fct + ![]() où
où ![]() est la phase au temps t = 0. Remarquons que la modulation angulaire
n'affecte pas l'amplitude la porteuse.
est la phase au temps t = 0. Remarquons que la modulation angulaire
n'affecte pas l'amplitude la porteuse.

![]() f /
f /![]() fmax, où
fmax, où
![]() fmax
est la valeur maximale de l'excursion de fréquence autorisée par les
règlements régissant le partage des fréquences, par exemple par le
Règlement des radiocommunications. Ainsi, en radiodiffusion sonore
à modulation de fréquence, on impose
fmax
est la valeur maximale de l'excursion de fréquence autorisée par les
règlements régissant le partage des fréquences, par exemple par le
Règlement des radiocommunications. Ainsi, en radiodiffusion sonore
à modulation de fréquence, on impose
![]() fmax = 75 [kHz].
fmax = 75 [kHz].
![]()