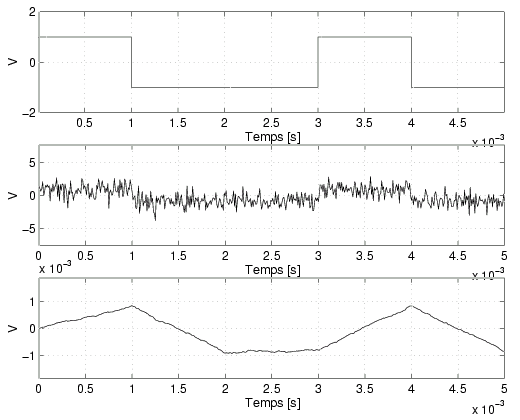
|
Le signal de bruit n(t) est un processus de bruit blanc à moyenne nulle et de densité spectrale de puissance N0/2. On suppose que le récepteur connaît la forme des ondes reçues de sorte que son comportement a pu être optimisé en fonction de ces ondes. L'incertitude résulte de l'addition du bruit n(t). La fonction du récepteur consiste à détecter la nature de l'impulsion g(t) sur base du signal x(t).
Le filtre étant supposé linéaire, la sortie peut s'exprimer sous la forme
| y(t) = gh(t) + nh(t) | (6.14) |

|
Une vue réaliste du problème consiste à exiger qu'à l'instant d'échantillonnage, la composante gh(t) soit la plus grande possible par rapport au bruit introduit par le canal, comme résultat du filtrage. Cela revient à choisir un filtre qui maximisera le rapport de puissance suivant
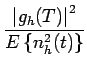 |
(6.15) |
où
![]() gh(T)
gh(T)![]() est la puissance instantanée
du signal filtré à l'instant d'échantillonnage T et
E
est la puissance instantanée
du signal filtré à l'instant d'échantillonnage T et
E![]() nh2(t)
nh2(t)![]() =
= ![]() mesure la puissance moyenne due au bruit à la sortie du filtre. Cherchons
donc à effectuer un choix judicieux du filtre h(t).
mesure la puissance moyenne due au bruit à la sortie du filtre. Cherchons
donc à effectuer un choix judicieux du filtre h(t).
Après de longs calculs, on montre que la valeur maximale vaut
| (6.16) |
cette dernière relation résultant du théorème de RAYLEIGH.
En d'autres termes, le rapport signal à bruit au moment de l'échantillonnage est fonction de l'énergie du signal d'entrée et de la puissance du bruit additif; la forme d'onde n'intervient pas directement mais bien son énergie.
Par contre, pour avoir le maximum correspondant à l'égalité, on a supposé que le filtre optimal correspond à
hopt(t) = 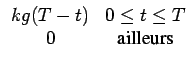 |
(6.18) |
En pratique, on dispose de plusieurs moyens de réaliser le filtre adapté:
| y(t) = |
(6.19) |
| y(t) = |
(6.20) |
| y[T] = |
(6.21) |
| z(t) = |
(6.22) |
| z(t) = |
(6.23) |