L'information analogique ne se prête pas telle quelle à un codage; il faut, au préalable, la transformer en numérique. La première étape d'une conversion analogique-numérique est le filtrage ou l'échantillonnage. Comme nous le verrons, ces deux opérations sont intimement liées.
On décrit généralement l'échantillonnage dans le domaine temporel. Il s'agit du processus par lequel un signal analogique est converti en une série d'échantillons également espacés. L'opération n'a d'intérêt que s'il s'avère possible de reconstituer le signal analogique à partir des échantillons, ce qui dépendra principalement de la cadence d'échantillonnage. L'étude de cette cadence optimale fait l'objet du théorème de SHANNON.
Considérons un signal g(t) d'énergie finie, connu pour tout temps
t. Supposons que l'on prenne un échantillon de ce signal à une
cadence régulière, soit un échantillon toutes les Ts secondes.
La séquence ainsi obtenue est notée
{g[nTs]}, avec
n ![]()
![]() où Ts est la période d'échantillonnage et son inverse,
fs = 1/Ts est la fréquence d'échantillonnage. Cette
forme d'échantillonnage est appelée échantillonnage instantané.
L'important théorème suivant lie la fréquence d'échantillonnage à
la valeur de la bande de base.
où Ts est la période d'échantillonnage et son inverse,
fs = 1/Ts est la fréquence d'échantillonnage. Cette
forme d'échantillonnage est appelée échantillonnage instantané.
L'important théorème suivant lie la fréquence d'échantillonnage à
la valeur de la bande de base.
| fs > 2W | (6.1) |
Pour démontrer cet important théorème, il suffit de noter que la fonction échantillonnée gs(t), définie par
| (6.3) |
| gs(t) |
(6.4) |
Sur le plan technique, l'importance du théorème tient à ceci: l'infinité continue des valeurs du signal analogique contient la même information que l'infinité dénombrable de ses échantillons. La fréquence minimale d'échantillonnage, soit 2W, est appelée fréquence de NYQUIST.
Il convient de remarquer que la contrainte fs > 2W est souvent
ramenée à
fs ![]() 2W. Il s'agit d'une erreur dans le cas de signaux
sinusoïdaux. Pour s'en convaincre, il suffit d'échantillonner une
sinusoïde de fréquence W à une fréquence 2W au droit de ses
passages par zéro. Tous les échantillons de cette séquence sont nuls
et il n'est dès lors pas possible de reconstituer la sinusoïde.
2W. Il s'agit d'une erreur dans le cas de signaux
sinusoïdaux. Pour s'en convaincre, il suffit d'échantillonner une
sinusoïde de fréquence W à une fréquence 2W au droit de ses
passages par zéro. Tous les échantillons de cette séquence sont nuls
et il n'est dès lors pas possible de reconstituer la sinusoïde.
Le spectre de la fonction échantillonnée reproduit certes le signal initial dans la bande de base mais il lui adjoint une infinité de copie centrée sur les multiples de la fréquence d'échantillonnage; c'est l'effet du train d'impulsions dans le domaine temporel. Pour reconstruire le signal original, il suffit d'utiliser un filtre passe-bas idéal de transmittance égale à Ts jusqu'à la fréquence de coupure fco, choisie supérieure à W.
Prenons donc un filtre passe-bas idéal de transmittance égale à 1 jusqu'à la fréquence de coupure f = fco. Ce filtre passe-bas idéal possède la réponse impulsionnelle suivante
2fco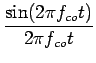 = 2fcosinc = 2fcosinc |
(6.5) |
Le signal reconstruit gr(t) résulte du passage de la fonction
échantillonnée au travers du filtre passe-bas idéal auquel, pour l'instant,
on attribue un gain A:
| gr(t) | = | gs(t) |
(6.6) |
| = | (6.7) | ||
| = | 2Afco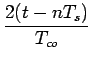 |
(6.8) |
Il s'agit d'une formule d'interpolation permettant de reconstituer la fonction g(t) à une constante près. Le théorème de WHITTAKER résulte du cas précis où le gain A et la fréquence de coupure fco valent respectivement Ts et fs/2.
L'interprétation suivante est immédiate (cf. figure 6.4):
sinc![]()
![]()
![]() est égal à 1 pour t = nTs
et égal à 0 pour tous les t = kTs tels que k
est égal à 1 pour t = nTs
et égal à 0 pour tous les t = kTs tels que k ![]() n. La somme
de la série 6.9 se réduit donc à g[nTs]
pour t = nTs. Le théorème signifie qu'entre ces valeurs cette
série interpole exactement g(t).
n. La somme
de la série 6.9 se réduit donc à g[nTs]
pour t = nTs. Le théorème signifie qu'entre ces valeurs cette
série interpole exactement g(t).
Dans la pratique, on opère sur des sommes finies telles
gN(t) = 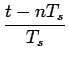 |
(6.10) |
gN(t) a les mêmes échantillons que g(t) pour | n| ![]() N,
mais
gN[nTs] = 0 pour | n|
N,
mais
gN[nTs] = 0 pour | n| ![]() N.
N.
L'établissement d'un cadre pour l'échantillonnage repose sur la propriété de largeur de bande limitée du signal g(t). En pratique, l'information n'est naturellement pas à bande limitée. La convolution par le train d'impulsions introduit alors un recouvrement entre bandes voisines dans le spectre; ce phénomène est appelé repli de spectre ou aliasing. L'opération de filtrage passe-bas s'avère incapable de supprimer ce recouvrement et on risque de voir apparaître, en raison du repli de spectre, une série de fréquences initialement absentes dans g(t). Deux approches suppriment ces effets indésirables:
En raison de la difficulté qu'il y a à réaliser un filtre ayant un flanc raide au droit de la fréquence de coupure, il est d'usage de définir une bande de garde dans laquelle la transition est plus douce. La bande de garde, typiquement de l'ordre de 10 à 20%, entraîne donc une augmentation de la fréquence d'échantillonnage. On parle parfois de la forme pratique du critère de NYQUIST, tenant compte de cette bande de garde
| fs = 2, 2W | (6.11) |
Exemple. Soit à produire une signal numérique à partir d'un signal musical s'étendant jusqu'à 20 [kHz]. En toute rigueur, une fréquence d'échantillonnage supérieure à 40 [kHz] suffit. Pour des questions de réalisation de filtre, on utilise plutôt 44, 1 [kHz] dans le standard du CD-Audio et même 48 [kHz] pour des signaux de qualité studio.
L'échantillonnage se fait en pratique avec une porte analogique qui
est un interrupteur fermé pendant une durée ![]() . Celle-ci doit
évidemment être très petite par rapport à Ts. En effet, le signal
échantillonné ainsi obtenu
g
. Celle-ci doit
évidemment être très petite par rapport à Ts. En effet, le signal
échantillonné ainsi obtenu
g![]() (t) est le produit, dans le
domaine temporel, de g(t) par un train ps(t) de rectangles
de largeur
(t) est le produit, dans le
domaine temporel, de g(t) par un train ps(t) de rectangles
de largeur ![]()
| ps(t) = p(t) |
(6.12) |
p(t) = 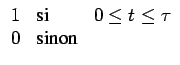 |
(6.13) |
La transformée de FOURIER de ps(t) étant
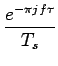 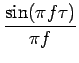 |
(6.14) |
Celle de
g![]() (t), parfois appelé signal échantillonné
naturel, vaut
(t), parfois appelé signal échantillonné
naturel, vaut
De ceci, on peut conclure que si la durée de fermeture de l'interrupteur
n'est pas infinitésimale, les spectres répétés sont affectés de coefficients
différents, bien que chacun d'eux reste une copie conforme de
![]() (f ).
La reconstruction à l'aide d'un filtre passe-bas reste donc correcte.
Bien entendu, il faut pour cela que l'interrupteur soit parfait, comme
on l'a supposé, c'est-à-dire qu'il ait une impédance nulle ou infinie
selon qu'il est fermé ou ouvert.
(f ).
La reconstruction à l'aide d'un filtre passe-bas reste donc correcte.
Bien entendu, il faut pour cela que l'interrupteur soit parfait, comme
on l'a supposé, c'est-à-dire qu'il ait une impédance nulle ou infinie
selon qu'il est fermé ou ouvert.
En pratique, il faut souvent saisir le signal à l'instant d'échantillonnage
et le maintenir dans une mémoire pendant un temps ![]() nécessaire
à l'exécution de certaines opérations de calcul. Le plus souvent,
cette mémoire est un condensateur.
nécessaire
à l'exécution de certaines opérations de calcul. Le plus souvent,
cette mémoire est un condensateur.
Il existe une assez grande variété de convertisseurs analogique-numérique (A/D, pour Analog-to-Digital).
Dans un système de télécommunications où l'information fait l'objet
d'un échantillonnage, le signal transmis a la forme d'un train d'impulsions.
Il existe différentes façons de présenter l'information sous la forme
d'une impulsion. Par exemple, on peut moduler l'amplitude d'un train
d'impulsions (PAM, Pulse Amplitude Modulation). On pourrait
de même conserver une amplitude constante à l'impulsion, mais rendre
sa largeur ![]() proportionnelle à l'échantillon (PDM, Pulse
Duration Modulation) ou encore, garder à l'impulsion une amplitude
et une largeur constante mais la décaler par rapport à son instant
d'arrivée théorique kTs d'un temps variable, proportionnel à
g[nTs], ce qui constitue une modulation de phase ou de position
(PPM, Pulse Position Modulation). Dans toutes ces méthodes,
la modulation d'impulsions reste analogique, en ce sens qu'un paramètre
continu est rendu proportionnel à l'échantillon. Comme d'après le
théorème de SHANNON, l'échantillonnage n'introduit aucune
erreur, ces méthodes permettent en théorie une transmission rigoureusement
fidèle de l'information. Elles ont en principe un avantage par rapport
à la transmission continue du signal d'information g(t): à puissance
moyenne égale, les impulsions ont une amplitude d'autant plus grande
que le rapport
proportionnelle à l'échantillon (PDM, Pulse
Duration Modulation) ou encore, garder à l'impulsion une amplitude
et une largeur constante mais la décaler par rapport à son instant
d'arrivée théorique kTs d'un temps variable, proportionnel à
g[nTs], ce qui constitue une modulation de phase ou de position
(PPM, Pulse Position Modulation). Dans toutes ces méthodes,
la modulation d'impulsions reste analogique, en ce sens qu'un paramètre
continu est rendu proportionnel à l'échantillon. Comme d'après le
théorème de SHANNON, l'échantillonnage n'introduit aucune
erreur, ces méthodes permettent en théorie une transmission rigoureusement
fidèle de l'information. Elles ont en principe un avantage par rapport
à la transmission continue du signal d'information g(t): à puissance
moyenne égale, les impulsions ont une amplitude d'autant plus grande
que le rapport
![]() /Ts est petit et elles peuvent d'autant mieux
être isolées du bruit. La contrepartie est cependant sévère car la
bande passante augmente dans des proportions inquiétantes.
/Ts est petit et elles peuvent d'autant mieux
être isolées du bruit. La contrepartie est cependant sévère car la
bande passante augmente dans des proportions inquiétantes.
Par exemple, pour un signal téléphonique limité à 3400 [Hz], on
pourrait prendre
fs = 8 [kHz], soit
Ts = 125 [![]() s]. Un
rapport
s]. Un
rapport
![]() /Ts = 0, 1 donne une durée de
/Ts = 0, 1 donne une durée de
![]() = 12, 5 [
= 12, 5 [![]() s],
ce qui exige une bande passante minimale de l'ordre de 50 [kHz]
si l'on veut plus ou mois respecter la forme des impulsions6.1. Cela ne constituerait pas nécessairement un inconvénient majeur,
car c'est une règle générale que l'élargissement du spectre apporte
une amélioration du rapport signal à bruit.
s],
ce qui exige une bande passante minimale de l'ordre de 50 [kHz]
si l'on veut plus ou mois respecter la forme des impulsions6.1. Cela ne constituerait pas nécessairement un inconvénient majeur,
car c'est une règle générale que l'élargissement du spectre apporte
une amélioration du rapport signal à bruit.
Aussi, les modulations analogiques d'un train d'impulsions n'ont-elles pas connu un très grand succès. Ce n'est pas le cas des modulations numériques comme on va le voir. En plus, une transmission d'impulsions sans en déformer la forme n'est pas une chose simple.
Dans un système de télécommunications où l'information fait l'objet d'un échantillonnage, on dispose d'un temps inférieur ou égal à la période d'échantillonnage Ts pour transmettre l'échantillon. Le signal transmis a donc la forme d'un train d'impulsions. Il existe diverses façons de présenter l'information sous la forme d'une impulsion.