Table des matières of 6.4 Modulation de la position des impulsions

Dans un système de modulation des impulsions, on peut représenter la valeur des échantillons par un autre paramètre que l'amplitude d'un train d'impulsions, tout comme dans le cas de modulation analogique il était possible de moduler, outre l'amplitude, la phase ou la fréquence. Si l'on conserve une amplitude constante à l'impulsion mais que sa largeur est rendue proportionnelle à l'échantillon, on obtient une modulation appelé Pulse-Duration Modulation (PDM); on parle aussi de pulse-width modulation ou encore de pulse-length modulation. La modulation affectera soit le début de l'impulsion, soit la fin, voire les deux extrémités.

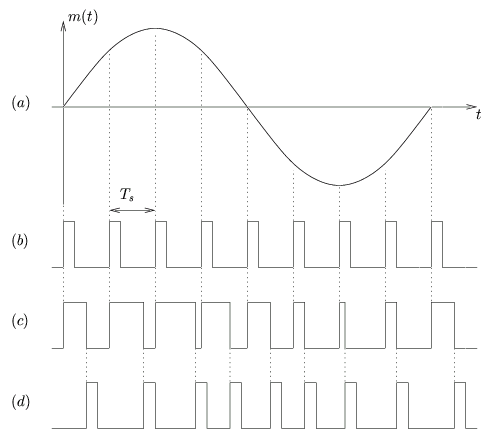
Le déplacement d'une extrémité de l'impulsion n'est pas gênant en soi, par contre la modulation PDM consomme une certaine puissance à transmettre un signal constant, non porteur d'information. En ne transmettant qu'une impulsion de courte durée au droit d'une transition du signal PDM, on fait l'économie de cette puissance; il s'agit d'une technique appelée pulse-position modulation (PPM). La figure 6.9 illustre les techniques de modulation précitées.

**Figure 6.9:** Un signal modulant, train d'impulsions à moduler, modulation PDM et modulation PPM.

Dans le cas d'une modulation PDM utilisant un signal p(t) de largeur $\tau$ variable, les impulsions voisines ne peuvent se chevaucher, ce que propose la condition suffisante suivante, à partir d'un signal modulant m(t),

p(t) $\displaystyle \neq$ 0, $\displaystyle \tau$ = k_p $\displaystyle \left\vert\vphantom{m(t)}\right.$ m(t) $\displaystyle \left.\vphantom{m(t)}\right\vert _{{\max}}^{}$ < $\displaystyle {\frac{{T_{s}}}{{2}}}$

(6.21)

s(t) = $\displaystyle \sum_{{n=-\infty}}^{{+\infty}}$ p(t - nT_s - k_pm[nT_s])

(6.22)

où p(t) est une impulsion centrée de largeur fixe $\tau$ . Pour éviter l'interférence entre symboles successifs, il faut respecter la condition suivante qui fait intervenir la largeur de l'impulsions

p(t) $\displaystyle \neq$ 0, k_p $\displaystyle \left\vert\vphantom{m(t)}\right.$ m(t) $\displaystyle \left.\vphantom{m(t)}\right\vert _{{\max}}^{}$ < $\displaystyle {\frac{{T_{s}}}{{2}}}$ - $\displaystyle {\frac{{\tau}}{{2}}}$

(6.23)

Plus k_p| m(t)|_max approche T_s/2, plus la forme de l'impulsion p(t) doit être étroite pour éviter l'interférence entre impulsions successives, et plus la bande occupée par le signal PPM sera large. À condition d'avoir une modulation sans interférence entre impulsions successives et un signal modulant m(t) à spectre limité, le respect du théorème de SHANNON garantit que l'on soit en mesure de reconstituer parfaitement le signal modulant m(t) à partir de s(t); la modulation PPM n'est pas source de distorsion.