6.5.1 Quantification

Définition 75   Le processus consistant à transformer un échantillon d'amplitude m[nT_s] d'un message m(t) pris au temps t = nT_s en une amplitude v[nT_s], choisie dans un ensemble fini de valeurs possibles, est appelé quantification.

On supposera l'instantanéité et l'absence de mémoire durant le processus de quantification, c'est-à-dire que la quantification d'un échantillon ne dépend pas de l'échantillon quantifié précédent ou suivant. C'est de loin la forme de quantification la plus répandue, bien que sous-optimale pour certains aspects.

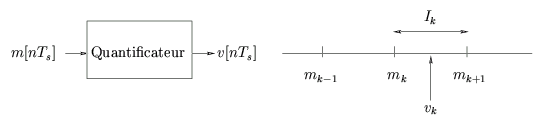
La modulation PCM consiste en ceci: à chaque instant d'échantillonnage, au lieu de transmettre la valeur exacte m[nT_s], on transmet le numéro d'ordre du niveau de quantification le plus proche. La figure 6.10 schématise la fonctionnement d'un quantificateur sans mémoire. Comme le montre le dessin de droite, les bornes m_k délimitent une série d'intervalle I_k =]m_k, m_k+1].

Figure 6.10: Description d'un quantificateur sans mémoire.

 

Dans un premier temps, un signal d'amplitude m appartenant à l'intervalle I_k =]m_k, m_k+1] est indicé par k ( k = 1, 2, ..., L). En sortie du quantificateur, l'indice k est transformé par une amplitude v_k ou par une suite de nombre, généralement en base binaire, significatives pour les valeurs contenues dans l'intervalle. Les valeurs représentatives v_k sont appelés niveaux représentatifs et la différence entre deux niveaux représentatifs successifs définit les intervalles ou pas de quantification. Les niveaux peuvent être équidistants ou non, la quantification étant dite linéaire ou non. En guise d'illustration, la figure 6.11 reprend l'ensemble des étapes d'une quantification de type PCM.

Figure 6.11: Échantillons instantanés, quantifiés et codes PCM.

 

La fonction caractéristique d'un organe de quantification, v = g(m), prend la forme d'une fonction en escaliers. Les deux alternatives, suivant que l'on transmette systématiquement le niveau représentatif immédiatement inférieur ou le plus proche, sont présentées à la figure 6.12.

Figure 6.12: Formes alternatives pour la fonction de quantification.

 

Il est clair qu'au travers d'une quantification, l'on commet une erreur d'arrondi. Le récepteur ne pourra jamais que reconstruire un signal v(t) à spectre limité et passant, aux instants d'échantillonnage, par les niveaux quantifiés.

L'erreur q(t) = v(t) - m(t) apparaît comme un bruit superposé au signal exact et appelé bruit de quantification^6.2. On ne peut le réduire qu'en choisissant un nombre de niveaux suffisants.

La bande passante requise pour la transmission des nombres issus des niveaux est évidemment beaucoup plus grande que celle qu'exigeait le signal initial. Par exemple, si l'on échantillonne exactement à la fréquence de NYQUIST f_s = 2W et si l'on utilise toute la durée de l'intervalle T_s pour transmettre les M bits du code, la bande requise est

$${\frac{{f_{s}}}{{2}}}$$ (6.24)

Mais, par rapport aux modulateurs analogiques d'impulsions, on a ici l'avantage que les impulsions du code peuvent être largement distordues, entachées de bruit ou d'interférence aussi longtemps que ces aléas n'entraînent pas d'erreurs sur les mots binaires. En plus, on bénéficie de toute la technologie des circuits intégrés et de l'informatique.

Outre les questions de réalisation, un certain nombre de problèmes doivent cependant être examinés:

• Calcul du rapport signal à bruit de quantification.
• Influence de la quantification non-linéaire.
• Problème de codage: faut-il utiliser un code binaire simple ou un autre code? En plus, il faut étudier la représentation des nombres binaires par des signaux électriques adaptés aux caractéristiques du canal de transmission (par exemple, si ce canal ne transmet pas le courant continu, le signal codé ne peut pas contenir de très basses fréquences).
• Problème de synchronisation. Il faut que le récepteur puisse repérer l'origine des mots binaires. Comment peut-on lui fournir cette information de cadrage? Ce problème se résout en ajoutant des bits supplémentaires (par exemple un bit valant toujours 1 en tête de chaque mot).
• Influence des erreurs de transmission.

Nous n'examinerons pas l'ensemble des questions précitées mais la question du bruit de quantification mérite d'être abordée.

Notes

... quantification^6.2

Le bruit gênant est le bruit qui se situe dans la bande de base; les bruits haute fréquence ne posent pas de problème.