|
On peut distinguer les principales catégories suivantes pour le codage linéaire de signaux PCM:
La comparaison de ces codes porte tant sur leurs performances que sur leur occupation spectrale. Dans un premier temps, nous allons déterminer l'occupation spectrale.
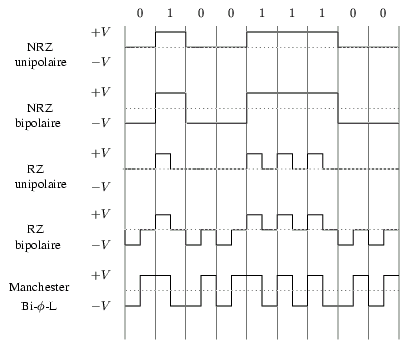
La manière la plus simple de transmettre un signal est d'utiliser deux niveaux de tension pour représenter les deux états binaires 0 et 1. La présence d'une tension peut, par exemple, représenter un 1 tandis que l'absence d'une tension représente un 0. C'est le cas du codage NRZ-L (Non Return to Zero Level) unipolaire. Cette technique, ainsi que d'autres, est illustrée à la figure 7.2.
La modélisation complète du codage NRZ unipolaire est résumée dans le tableau suivant:
| Symbole | Probabilité | Ak | Onde |
| 0 | 1 - p | 0 | ... |
| 1 | p | V |
1, 0 |
Pour calculer la densité spectrale de puissance du signal mis en forme, on calcule la moyenne, la variance ainsi que la transformée de FOURIER du signal de mise en forme.
Moyenne
| (7.39) |
Variance
| (7.40) |
Filtre
![]()
![]() (f )
(f )![]() = T2
= T2![]()
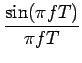
![]()
(7.41)
Comme les symboles sont non-corrélés, il advient
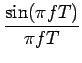 |
(7.42) |
La densité spectrale est donc en forme de sinus cardinal avec une
composante continue importante7.3. Le fait que
![]() (f ) soit nulle pour f = k/T rend la synchronisation
difficile car il n'y a pas de composante rythmée à la cadence d'émission
binaire.
(f ) soit nulle pour f = k/T rend la synchronisation
difficile car il n'y a pas de composante rythmée à la cadence d'émission
binaire.
Le spectre du signal mis en forme est infini. En théorie donc, il faudrait une bande passante infinie, ce qui n'est pas acceptable. Afin de définir une largeur pratique de bande, examinons les graphes de la figure 7.3.
Le premier graphe montre la densité spectrale
![]() (f ). Le second
reprend la valeur de la puissance cumulée comprise dans la bande [0, fT].
Cette puissance vaut 84%, 91,3% et 95% respectivement pour fT = 0, 6,
fT = 1 et fT = 2. Un choix pratique consiste à prendre une largeur
de bande égale à
(f ). Le second
reprend la valeur de la puissance cumulée comprise dans la bande [0, fT].
Cette puissance vaut 84%, 91,3% et 95% respectivement pour fT = 0, 6,
fT = 1 et fT = 2. Un choix pratique consiste à prendre une largeur
de bande égale à
![]() .
.
Le codage NRZ bipolaire s'étudie suivant la même démarche à partir de la représentation suivante:
| Symbole | Probabilité | Ak | Onde |
| 0 | 1 - p | - V |
1, 0 |
| 1 | p | V |
1, 0 |
Moyenne
| (7.43) |
Variance
| = | E |
(7.44) | |
| = | V2p + V2(1 - p) - V2(2p - 1)2 | (7.45) | |
| = | 4p(1 - p)V2 | (7.46) |
Filtre
![]()
![]() (f )
(f )![]() = T2
= T2![]()
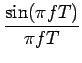
![]()
(7.47)
Comme les symboles sont non-corrélés, il advient
| = | 4p(1 - p)V2T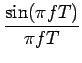 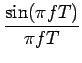 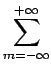 |
||
| = | 4p(1 - p)V2T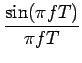 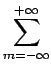 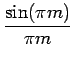 |
||
| = | 4p(1 - p)V2T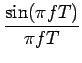 |
(7.48) |
Dans le cas fort théorique de deux symboles totalement équiprobables, il n'y a pas de composante continue dans le spectre de puissance. Par contre, on observe un résidu de composante continue pour des symboles non équiprobables. Remarquons aussi qu'en toute logique, le niveau moyen de puissance d'un signal NRZ bipolaire est supérieur de 6 [dB] à celui d'un codage NRZ unipolaire.
Le codage NRZ a la particularité de représenter une longue série de 0 par un signal continu, ce qui le rend sensibles aux bruits parasites. De plus, la synchronisation sur les variations peut facilement être perdue lorsqu'il n'y a pas de variation pendant un certain laps de temps.
Le codage NRZ-M (Non Return to Zero Mark) est une variante du codage NRZ-L qui consiste à inverser la polarité à chaque valeur binaire 1. Il permet d'éviter l'absence de transitions, à condition d'assurer également l'absence de rafales de 0.
Comme son nom l'indique, le codage RZ ramène le signal à une tension nulle pendant tout intervalle T. On a ainsi la certitude d'avoir régulièrement des transitions, mais il faut en payer le prix car la présence de deux transitions par période T entraîne le doublement de la bande passante ce que confirme le développement théorique suivant.
Soit le signal de mise en forme que voici:
| Symbole | Probabilité | Ak | Onde |
| 0 | 1 - p | 0 | ... |
| 1 | p | V | pour
t |
Moyenne
| (7.49) |
Variance
| (7.50) |
Filtre
![]()
![]() (f )
(f )![]() =
= ![]() T2
T2![]()
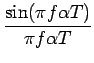
![]()
(7.51)
Comme les symboles sont non-corrélés, il advient
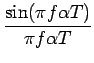 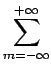 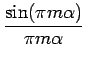 |
(7.52) |
Si on prend
![]() =
= ![]() , ce qui est le choix habituel,
, ce qui est le choix habituel,
| = | 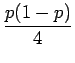 V2T V2T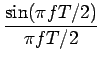 |
||
+ 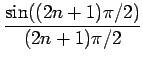 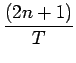 ) ) |
(7.53) | ||
| = | 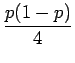 V2T V2T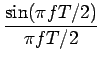 |
||
+ p2V2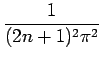 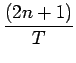 ) ) |
(7.54) |
| Symbole | Probabilité | Ak | Onde |
| 0 | 1 - p | - V | pour
t |
| 1 | p | V | pour
t |
Moyenne
| (7.55) |
Variance
| (7.56) |
Filtre
![]()
![]() (f )
(f )![]() =
= ![]() T2
T2![]()
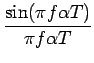
![]()
(7.57)
| = | 4p(1 - p)V2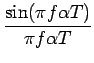 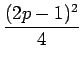 V2 V2 |
||
+ (2p - 1)2V2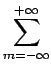 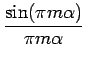 |
(7.58) |
| = | p(1 - p)V2T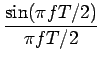 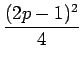 V2 V2 |
(7.59) | |
+ (2p - 1)2V2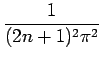 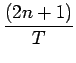 ) ) |
(7.60) |
Le code MANCHESTER est de type biphasé, c'est-à-dire qu'un bit d'information est représenté par une transition de tension en milieu de période. La valeur 0 est représentée par un front montant, et la valeur 1 par un front descendant. Cette transition sert également de référence pour l'horloge.
| Symbole | Probabilité | Ak | Onde | ||||
| 0 | 1 - p | - V |
|
||||
| 1 | p | V |
|
Moyenne
| (7.61) |
Variance
| (7.62) |
Filtre
![]() (f )=
(f )= ![]()
![]()
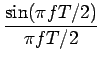
![]()
![]() - e-2
- e-2![]() jfT/4 + e+2
jfT/4 + e+2![]() jfT/4
jfT/4![]() = T
= T![]()
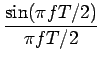
![]() j sin(
j sin(![]() fT/2)
fT/2)
(7.63)
![]()
![]() (f )
(f )![]() = T2
= T2![]()
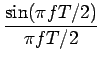
![]() sin2(
sin2(![]() fT/2)
fT/2)
(7.64)
| = | 4p(1 - p)V2T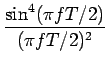 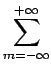 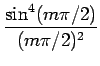 |
||
| = | 4p(1 - p)V2T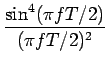 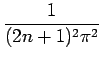 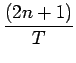 ) ) |
Les codages biphasés ont la particularité de nécessiter deux transitions pour un bit d'information (1B/2T). La fréquence du signal doit donc être le double de la bande passante offerte au réseau local. Par exemple, les composants d'un réseau Ethernet, qui utilisent un codage MANCHESTER, sont cadencés à 20 [MHz] afin d'offrir le 10 [Mb/s] de débit.
Le tableau 7.2 reprend les spectres des signaux précités. Il permet de comparer l'utilisation de la bande passante, la présence ou non de raies à la fréquence d'émission et l'amplitude absolue des spectres.
|
Le codage de MANCHESTER différentiel est une variante du précédent. Il consiste à assurer deux transitions pour un symbole 0 et une seule pour un symbole 1. Le standard Token-Ring 802.5 y recourt.
On peut également citer le codage HDB3 (High-Density Bi-polar modulus 3) qui est utilisé sur les liaisons de modulation par impulsions codées des réseaux téléphoniques. Il a pour caractéristique de limiter à trois le nombre de zéros successifs.
De nouveaux codages liés aux technologies xDSL (x Digital Subscriber Loop) sont apparues récemment; il s'agit notamment de CAP (Carrierless Amplitude Phase) dans les versions CAP12, CAP16 et CAP64, de QAM25 (Quadrature Amplitude Modulation) et PAM5.
En fait, il existe de très nombreuses variantes de codage en ligne d'émission.
De par leur nature, ces codages supposent une meilleure qualité de transmission, notamment obtenue par fibre optique, car ils sont sensibles aux parasites. Les signaux utilisés sont à trois états (ternaires) ou à quatre états (quaternaires). Le codage 4B/3T permet ainsi de coder 4 bits d'information en 3 signaux ternaires. Il est, par exemple, utilisé sur le bus S0 du RNIS.
La codage 2B/1Q permet de coder 2 bits d'information en un signal quaternaire. Il est utilisé sur le bus S0 du RNIS aux États-Unis. Le tableau 7.3 présente le système employé.
Le codage 4B/5T, plus performant, est utilisé dans les réseaux FDDI. Un débit de 100 [Mb/s] peut donc être véhiculé par un signal à 125 [MHz]. Cette technique consiste à représenter 4 bits consécutifs par un signal composé de 5 transitions.
Les codages complets entraînent une implémentation plus complexe que les codages en ligne car ils sont plus sensibles à la diaphonie et offrent un rapport signal à bruit moins élevé. Par contre, ils permettent de diminuer la fréquence du signal de transmission grâce à une plus grande redondance d'information. Le codage 1B/1Q permet ainsi d'offrir une bande passante double de la fréquence du signal, et donc de diminuer le coût des composants.
La qualité d'un codage se mesure entre autres par son taux d'interférence entre symboles transmis. L'interférence provient du fait que la forme de l'onde d'un symbole affecte la suivante. Ainsi le 2B/1Q a un plus grand taux d'interférence que le 4B/3T car la forme des signaux est moins riche.
Les codages complets sont généralement associés à des codages en ligne, notamment sur des supports en cuivre qui sont sujets aux perturbations électromagnétiques. Par exemple, les réseaux ATM utilisent une association 4B/5T+NRZI.