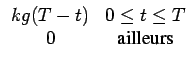Sous-sections
Le signal de bruit n(t) est un processus de bruit blanc à moyenne
nulle et de densité spectrale de puissance N0/2. On suppose
que le récepteur connaît la forme des ondes reçues de sorte que son
comportement a pu être optimisé en fonction de ces ondes. L'incertitude
résulte de l'addition du bruit n(t). La fonction du récepteur consiste
à détecter la nature de l'impulsion g(t) sur base du signal x(t).
Le filtre étant supposé linéaire, la sortie peut s'exprimer sous la
forme
| y(t) = gh(t) + nh(t) |
(7.68) |
où gh(t) et nh(t) représentent les contributions dues
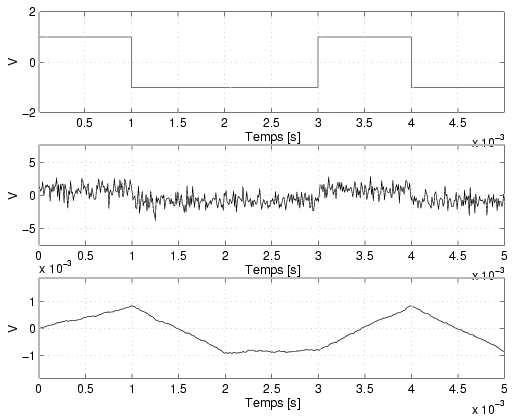
respectivement à g(t) et n(t). Le signal y(t) est illustré
à la figure 7.7.
Figure 7.7:
Signaux intervenant au cours de la démodulation d'un signal numérique
en bande de base: le signal original, le signal à l'entrée du récepteur
et le signal à la sortie du filtre.
|
|
Une vue réaliste du problème consiste à exiger qu'à l'instant d'échantillonnage,
la composante gh(t) soit la plus grande possible par rapport
au bruit introduit par le canal, comme résultat du filtrage. Cela
revient à choisir un filtre qui maximisera le rapport de puissance
suivant
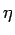 = = 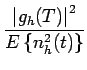 |
(7.69) |
où
 gh(T)
gh(T)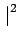 est la puissance instantanée
du signal filtré à l'instant d'échantillonnage T et
E
est la puissance instantanée
du signal filtré à l'instant d'échantillonnage T et
E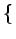 nh2(t)
nh2(t)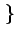 =
= 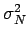 mesure la puissance moyenne due au bruit à la sortie du filtre. Cherchons
donc à effectuer un choix judicieux du filtre h(t).
mesure la puissance moyenne due au bruit à la sortie du filtre. Cherchons
donc à effectuer un choix judicieux du filtre h(t).
Comme
gh(t) = 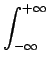 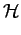 (f ) (f )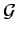 (f )e2 (f )e2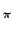 jftdf jftdf |
(7.70) |
le numérateur de 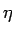 vaut
vaut
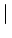 gh(T) gh(T) = =  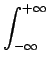 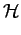 (f ) (f )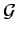 (f )e2 (f )e2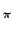 jfTdf jfTdf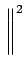 |
(7.71) |
Il reste à déterminer le dénominateur de 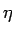 : la puissance de
bruit. On sait que
: la puissance de
bruit. On sait que
par application du théorème de WIENER-KINTCHINE.
Dès lors
E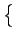 nh2(t) nh2(t)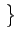 |
= |
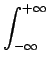 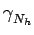 (f )df (f )df |
(7.73) |
| |
= |
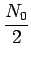 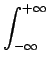 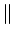 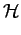 (f ) (f )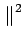 df df |
(7.74) |
L'inégalité de SCHWARZ établit que si
et
alors
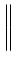 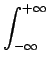 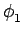 (x) (x)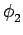 (x)dx (x)dx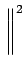 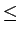 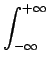  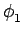 (x) (x)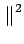 dx dx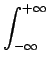 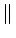 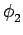 (x) (x)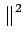 dx dx |
(7.77) |
Par ailleurs, l'égalité tient à la condition que
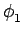 (x) = k (x) = k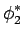 (x) (x) |
(7.78) |
Dans le cas présent,
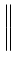 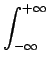 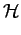 (f ) (f )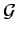 (f )e2 (f )e2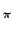 jfTdf jfTdf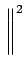 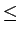 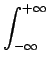 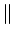 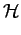 (f ) (f )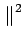 df df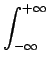 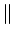 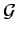 (f ) (f )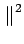 df df |
(7.79) |
Le rapport à maximiser
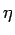 = = 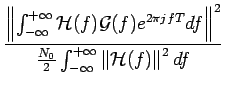 |
(7.80) |
devient donc
D'où la valeur maximale
où l'on a défini l'énergie du signal d'entrée
par
cette dernière relation résultant du théorème de RAYLEIGH.
En d'autres termes, le rapport signal à bruit au moment de l'échantillonnage
est fonction de l'énergie du signal d'entrée et de la puissance du
bruit additif; la forme d'onde n'intervient pas directement mais bien
son énergie.
Par contre, pour avoir le maximum correspondant à l'égalité, on a
supposé que (cf. relation 7.78)
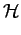 opt(f )= k opt(f )= k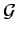 *(f )e-2 *(f )e-2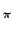 jfT jfT |
(7.84) |
et donc
hopt(t) = k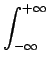 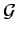 *(f )e-2 *(f )e-2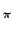 jf(T-t)df jf(T-t)df |
(7.85) |
Comme pour un signal réel g(t),
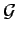 *(f )=
*(f )= 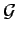 (- f ),
on a
(- f ),
on a
| hopt(t) |
= |
k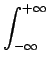 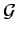 (- f )e-2 (- f )e-2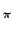 jf(T-t)df jf(T-t)df |
(7.86) |
| |
= |
kg(T - t) |
(7.87) |
On peut donc écrire le filtre optimal par
hopt(t) = 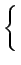 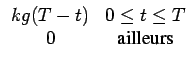 |
(7.88) |
À une amplitude près, le filtre optimal, appelé filtre adapté,
correspond à l'onde de mise en forme retournée sur la période T.
En pratique, on dispose de plusieurs moyens de réaliser le filtre
adapté:
- Par convolution. C'est l'implémentation directe de la formule
de filtrage
y(t) = 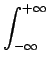 x( x( )h(t - )h(t -  )d )d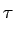 |
(7.89) |
On échantillonne ce signal à l'instant t = T pour obtenir la valeur
y[T].
- Par corrélation. Considérons l'expression de y(t)
y(t) = 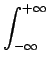 x( x(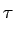 )g(T - t + )g(T - t + 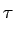 )d )d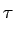 |
(7.90) |
à partir de quoi
Par faciliter les calculs, on préfère le signal
En t = T, les deux signaux sont égaux même si ailleurs
y(t) 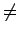 z(t).
Cela importe peu car c'est la valeur au droit de l'échantillonnage
qui nous intéresse.
z(t).
Cela importe peu car c'est la valeur au droit de l'échantillonnage
qui nous intéresse.
- Par intégration. Dans le cas particulier d'un fonction g(t) = 1
sur [0, T], la formule de z(t) se réduit à
Il s'agit donc d'un simple intégrateur qu'on échantillonnera
en t = T.
Quand l'allure de l'onde de mise en forme s'y prête, l'intégrateur
est souvent choisi pour l'implémentation. Il convient néanmoins de
remarquer que l'intégrateur doit être remis à 0 après chaque échantillonnage
sous peine d'une dérive de la valeur de z(t).
Marc Van Droogenbroeck. Tous droits réservés.
2005-03-11

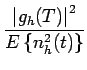
![]() gh(T)
gh(T)![]() est la puissance instantanée
du signal filtré à l'instant d'échantillonnage T et
E
est la puissance instantanée
du signal filtré à l'instant d'échantillonnage T et
E![]() nh2(t)
nh2(t)![]() =
= ![]() mesure la puissance moyenne due au bruit à la sortie du filtre. Cherchons
donc à effectuer un choix judicieux du filtre h(t).
mesure la puissance moyenne due au bruit à la sortie du filtre. Cherchons
donc à effectuer un choix judicieux du filtre h(t).
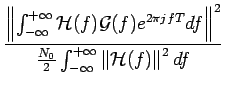
![]() *(f )=
*(f )= ![]() (- f ),
on a
(- f ),
on a