Table des matières of 3.2.4 Réalisation de la modulation d'amplitude classique

Il existe de nombreux circuits de réalisation de la modulation d'amplitude classique. Il n'entre pas dans notre intention d'étudier les technologies, par ailleurs dépendantes de la fréquence, ou de détailler l'ensemble des schémas possibles. Seuls seront présentés les principes de réalisation avec quelques circuits en guise d'illustration. L'organe de base pour réaliser une modulation d'amplitude est le mélangeur; il combine deux fréquences pour en créer la somme et la différence.

Deux approches sont possibles. Elles sont connues sous les noms de modulations linéaire ou quadratique.

3.2.4.1 Modulation linéaire

Le principe de la modulation linéaire est illustré à la figure 3.5. La porteuse est amplifiée dans un dispositif électronique dont le gain g(t) est réglable et est une fonction linéaire du signal modulant.

**Figure 3.5:** Principe de la modulation linéaire.

Le multiplieur est l'élément conceptuellement le plus immédiat pour implémenter la modulation d'amplitude. Comme son nom l'indique, le multiplieur effectue le produit des signaux fournis à l'entrée.

Il existe de nombreux types de multiplieurs analogiques sous forme intégrée, qui peuvent multiplier des tensions alternatives (multiplieur quatre quadrants) ou seulement des tensions positives (multiplieur deux quadrants). Le multiplieur est un premier type de mélangeur. La sortie d'un multiplieur peut s'écrire

s(t) = kc(t)g(t) + k'c(t) + k''g(t) + k'''

(3.22)

Après compensation des distorsions et décalages éventuels, on obtient la relation linéaire d'un multiplieur parfait

s(t) = kc(t)g(t)

(3.23)

La dénomination de modulation linéaire vient de ce que la loi régissant le gain du dispositif en fonction du signal modulant doit être absolument linéaire; en effet, une loi non-linéaire reviendrait à causer de la distorsion non-linéaire sur le signal d'information, ce qui est généralement inacceptable.

3.2.4.2 Modulation quadratique

Le principe de la modulation quadratique est le suivant: la porteuse c(t) = A_ccos(2 $\pi$ f_ct) et le signal modulant x(t) = x_maxm(t) sont d'abord additionnés, et le résultat est appliqué à un organe non-linéaire. Un filtre passe-bande est utilisé pour éliminer les composantes spectrales indésirables à la sortie de celui-ci (figure 3.6).

**Figure 3.6:** Principe de la modulation quadratique.

Supposons que la fonction de réponse de l'organe non-linéaire soit r(t) et possède un développement en série de TAYLOR. On peut alors écrire

r(x(t) + c(t)) = r₀ + r₁(x(t) + c(t)) + r₂(x(t) + c(t))² + r₃(x(t) + c(t))³ +...

(3.24)

r(x(t) + c(t)) = r₀ + r₁x(t) + r₁(1 + $\displaystyle {\frac{{2r_{2}}}{{r_{1}}}}$ x_maxm(t))c(t) + r₂x²(t) + r₂c²(t) +...

(3.25)

Dans les conditions normales, f_c est beaucoup plus grande que la bande de base, et les termes de la somme sont très nettement disjoints sur l'axe des fréquences. Le troisième terme donne les composantes spectrales correspondant à la modulation d'amplitude classique et peut donc être aisément sélectionné par le filtre passe-bande représenté à la figure 3.6. Le terme donnant les bandes latérales provient du terme quadratique dans le développement en série de TAYLOR de la non-linéarité. D'où le nom de modulation quadratique. Les termes non écrits donnent lieu à des composantes spectrales à af_c±bW qui peuvent toutes être éliminées par filtrage, à un exception près: il s'agit des termes à f_c±bW qui recouvrent la bande utile. Ces termes correspondent à une distorsion affectant l'amplitude instantanée du signal résultant, c'est-à-dire à une distorsion non-linéaire sur le signal modulant. Cela est donc hautement indésirable si ce signal est du type analogique, et acceptable dans certaines proportions pour des signaux numériques. Une analyse plus fine montre que les composantes indésirables proviennent des termes d'ordre impair et supérieur ou égal à trois. La modulation quadratique exige donc que ces termes soient absents du développement; idéalement la caractéristique de la non-linéarité ne devrait comporter que le terme linéaire et quadratique. La suppression des termes d'ordre impair s'obtient généralement par une architecture symétrique et balancée du modulateur non-linéaire.

Une non-linéarité très proche du comportement quadratique désiré est la relation liant le courant de drain i_d et la tension v_gs entre la grille et la source dans un transistor à effet de champ en zone de saturation i_d = i_t(1 - (v_gs/v_p)²).

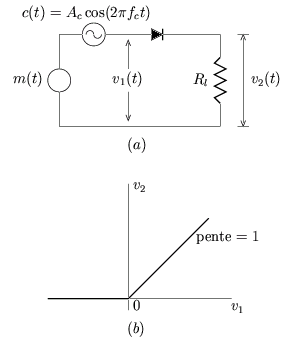
De nombreux circuits de modulation, dont celui de la figure 3.7, utilisent une diode.

**Figure 3.7:** Modulateur AM à diode: (a) circuit électronique, (b) caractéristique idéalisée d'entrée-sortie.

Considérons le circuit de la partie supérieure de la figure 3.7. On suppose que l'amplitude de la porteuse est telle qu'elle entraîne une large excursion sur la fonction caractéristique de la diode. Pour la facilité de l'analyse, le fonctionnement de la diode est modélisé par celui d'un interrupteur idéal: l'impédance est nulle lorsque la diode laisse passer un courant induit par la tension appliquée à ses bornes, c'est-à-dire lorsque c(t) > 0. Dans ce cas, la tension relevée aux bornes de la résistance de charge R_l suit parfaitement la tension v₁(t); autrement dit, la combinaison diode-résistance présente l'allure d'une fonction de transfert linéaire telle que représentée à la figure 3.7.(b).

Le signal v₁(t) consiste en la somme de la porteuse c(t) = A_ccos $\left(\vphantom{2\pi f_{c}t}\right.$ 2 $\pi$ f_ct $\left.\vphantom{2\pi f_{c}t}\right)$ et du signal modulant m(t):

v₁(t) = A_ccos $\displaystyle \left(\vphantom{2\pi f_{c}t}\right.$ 2 $\displaystyle \pi$ f_ct $\displaystyle \left.\vphantom{2\pi f_{c}t}\right)$ + m(t)

(3.26)

**Figure 3.8:** Train d'impulsions périodiques.

Si l'amplitude de la porteuse A_c est telle que $\left\vert\vphantom{m(t)}\right.$ m(t) $\left.\vphantom{m(t)}\right\vert$ $\ll$ A_c, la tension v₂(t) vaut

v₂(t) 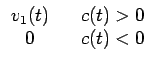$\displaystyle \simeq$ $\displaystyle \left\{\vphantom{ \begin{array}{ccc} v_{1}(t) & & c(t)>0\\ 0 & & c(t)<0\end{array}}\right.$ $\displaystyle \begin{array}{ccc} v_{1}(t) & & c(t)>0\\ 0 & & c(t)<0\end{array}$

(3.27)

Dès lors, le signal v₂(t) oscille entre v₁(t) et 0 à la fréquence de porteuse f_c. On peut réécrire v₂(t) sous la forme du produit suivant

v₂(t) $\displaystyle \simeq$ $\displaystyle \left[\vphantom{A_{c}\,\cos\left(2\pi f_{c}t\right)+m(t)}\right.$ A_c cos $\displaystyle \left(\vphantom{2\pi f_{c}t}\right.$ 2 $\displaystyle \pi$ f_ct $\displaystyle \left.\vphantom{2\pi f_{c}t}\right)$ + m(t) $\displaystyle \left.\vphantom{A_{c}\,\cos\left(2\pi f_{c}t\right)+m(t)}\right]$ p_{T_c}(t)

(3.28)

où p_{T_c}(t) est un train d'impulsions de période T_c = 1/f_c. En introduisant l'expression de la série de FOURIER de p_{T_c}(t), à savoir,

p_{T_c}(t) = $\displaystyle {\frac{{1}}{{2}}}$ + $\displaystyle {\frac{{2}}{{\pi}}}$ $\displaystyle \sum_{{n=1}}^{{\infty}}$ $\displaystyle {\frac{{\left(-1\right)^{n-1}}}{{2n-1}}}$ cos $\displaystyle \left[\vphantom{2\pi f_{c}t\left(2n-1\right)}\right.$ 2 $\displaystyle \pi$ f_ct $\displaystyle \left(\vphantom{2n-1}\right.$ 2n - 1 $\displaystyle \left.\vphantom{2n-1}\right)$ $\displaystyle \left.\vphantom{2\pi f_{c}t\left(2n-1\right)}\right]$

(3.29)

dans l'équation 3.28, v₂(t) s'écrit comme la somme des deux composantes suivantes:

3.2.4.3 Contrôle de la modulation

Pour contrôler la linéarité de la caractéristique de modulation et l'absence de surmodulation, on peut appliquer le signal modulé s(t) à l'entrée Y d'un oscilloscope, tandis que la tension modulante x(t) est appliquée en X. On obtient un figure trapézoïdale (figure 3.9) dont les côtés donnent la caractéristique de modulation. Cette méthode s'applique tout aussi bien à la modulation à porteuse supprimée.