Table des matières of 3.2.5 Démodulateurs

De même que l'on pouvait mettre en oeuvre deux principes (linéaire et quadratique) pour réaliser la modulation, il existe plusieurs manières de faire la démodulation, aussi appelée détection depuis les débuts de la radio; à l'époque, on travaillait en MORSE (A1) et démoduler le signal revenait à détecter la présence ou l'absence de la porteuse.

3.2.5.1 Détection d'enveloppe

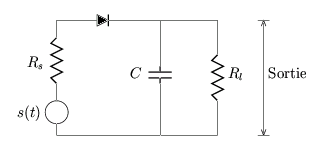
La détection d'enveloppe ou détection de crête est le principe de réalisation de démodulateur le plus courant et le plus simple pour les signaux modulés en amplitude avec porteuse. Son schéma est donné à la figure 3.10.

Le détecteur d'enveloppe est composé d'une diode et d'un filtre RC. Son fonctionnement est le suivant. Lors du demi-cycle positif du signal d'entrée s(t), la diode est polarisée en direct et la capacité C se charge rapidement à la valeur de crête du signal d'entrée. Quand le signal d'entrée chute en-dessous de cette valeur, la diode est polarisée en inverse et la capacité se décharge lentement dans la résistance R_l. La décharge se poursuit jusqu'au demi-cycle positif suivant du signal d'entrée. Quand celui-ci devient plus grand que la tension aux bornes de la capacité, la diode conduit à nouveau et le processus recommence.

Nous supposons que la diode est idéale, présentant une résistance r_f au passage du courant lorsqu'elle est polarisée en direct et une résistance infinie lorsqu'elle est polarisée en inverse. Nous supposerons également que le système générant le signal modulé s(t) présente une impédance interne R_s. La constante de temps de charge (lors du demi-cycle positif du signal d'entrée) $\left(\vphantom{r_{f}+R_{s}}\right.$ r_f + R_s $\left.\vphantom{r_{f}+R_{s}}\right)$ C doit être petite par rapport à la période de la porteuse 1/f_c, c'est-à-dire

$\displaystyle \left(\vphantom{r_{f}+R_{s}}\right.$ r_f + R_s $\displaystyle \left.\vphantom{r_{f}+R_{s}}\right)$ C $\displaystyle \ll$ $\displaystyle {\frac{{1}}{{f_{c}}}}$

de telle sorte que la capacité C se charge rapidement et suive, lorsque la diode conduit, la tension d'entrée lorsque celle-ci croît rapidement.

D'un autre côté, la constante de temps de décharge R_lC (lorsque la diode est bloquée) doit être assez grande pour assurer une décharge lente de la capacité au travers de R_l entre deux demi-cycles positifs du signal d'entrée. Mais la tension aux bornes de la capacité doit suivre l'enveloppe du signal d'entrée même quand celle-ci diminue. Donc la constante de temps de décharge R_lC doit être suffisamment petite pour pouvoir suivre la descente de l'enveloppe et donc de m(t). En conclusion, nous devons avoir

$\displaystyle {\frac{{1}}{{f_{c}}}}$ $\displaystyle \ll$ R_lC $\displaystyle \ll$ $\displaystyle {\frac{{1}}{{W}}}$

3.2.5.2 Démodulation AM synchrone ou cohérente

On peut retrouver le signal modulant à partir du signal modulé avec porteuse en multipliant s(t) par une cosinusoïde identique en fréquence et en phase à celle de la porteuse. En effet,

s(t)cos(2 $\displaystyle \pi$ f_ct)	=	$\displaystyle {\frac{{A_{c}}}{{2}}}$ (1 + k_am(t))(1 + cos(4 $\displaystyle \pi$ f_ct))	(3.31)
	=	$\displaystyle {\frac{{A_{c}}}{{2}}}$ $\displaystyle \left(\vphantom{1+k_{a}m(t)}\right.$ 1 + k_am(t) $\displaystyle \left.\vphantom{1+k_{a}m(t)}\right)$ + $\displaystyle {\frac{{A_{c}}}{{2}}}$ $\displaystyle \left(\vphantom{\cos(4\pi f_{c}t)+k_{a}m(t)\cos(4\pi f_{c}t)}\right.$ cos(4 $\displaystyle \pi$ f_ct) + k_am(t)cos(4 $\displaystyle \pi$ f_ct) $\displaystyle \left.\vphantom{\cos(4\pi f_{c}t)+k_{a}m(t)\cos(4\pi f_{c}t)}\right)$	(3.32)

On peut donc réaliser la démodulation en faisant le produit du signal modulé par la porteuse, ce qui peut se faire avec le même type de circuit que la modulation, par exemple un modulateur en anneau dont les diodes seraient commandées par un générateur de porteuse local. Dans l'expression 3.32, le premier terme restitue en effet le signal modulant (avec une composante continue indésirable), tandis que le deuxième correspond à une raie flanquée de bandes latérales de part et d'autre de la fréquence double 2f_c et peut aisément être éliminé par un filtre passe-bas. Le schéma correspondant est montré à la figure 3.11.

Si le circuit de démodulation proprement dit est d'une simplicité élémentaire, il faut néanmoins résoudre le délicat problème de la création locale de la porteuse servant à la démodulation. Si l'on produit la porteuse locale à l'aide d'un oscillateur, il y a fort à craindre que ce signal n'ait pas exactement la même fréquence et la même phase que la porteuse utilisée pour le signal modulé. Pour clarifier la situation, supposons que cet oscillateur produise un signal A'cos(2 $\pi$ f_lt + $\phi$ ). Le produit de ce signal par le signal réceptionné, à porteuse supprimé (pour la simplicité des propos), vaut

s(t)A'cos(2 $\displaystyle \pi$ f_lt + $\displaystyle \phi$ ) = $\displaystyle {\frac{{A_{c}A'}}{{2}}}$ m(t)(cos(2 $\displaystyle \pi$ (f_l - f_c)t + $\displaystyle \phi$ ) + cos(2 $\displaystyle \pi$ (f_c + f_l)t + $\displaystyle \phi$ ))

(3.33)

Tout écart entre la fréquence de l'oscillateur local et la fréquence de porteuse entraîne une dérive dans le calcul du signal démodulé. De plus, à supposer que les fréquences f_l et f_c concordent parfaitement, l'écart de phase joue l'effet d'un atténuateur car, après filtrage,

s(t)A'cos(2 $\displaystyle \pi$ f_lt + $\displaystyle \phi$ ) $\displaystyle \rightarrow$ $\displaystyle {\frac{{A_{c}A'}}{{2}}}$ m(t)cos $\displaystyle \phi$

(3.34)