Table des matières of 3.2.10 Modulation à bande latérale unique

Si la modulation en quadrature économise la moitié de la bande passante, elle a l'inconvénient de nécessiter la création des deux signaux, m₁(t) et m₂(t), à partir d'un signal à transmettre m(t). Une alternative consiste à supprimer une bande latérale; on obtient alors une modulation à bande latérale unique (Single Sideband, SSB). Cette technique est abondamment utilisée pour la transmission de signaux de télévision, gros consommateurs de bande passante (un signal de qualité PAL nécessite de l'ordre de 5 à 8 [MHz]).

3.2.10.1 Filtrage d'une bande

Soit à filtrer le signal u(t) = A_cm(t)cos(2 $\pi$ f_ct) dont on ne désire garder qu'une bande. On fait passer le signal à travers un filtre de transmittance $\mathcal {H}$ (f ). En sortie, le signal vaut

$\displaystyle \mathcal {S}$ (f )	=	$\displaystyle \mathcal {U}$ (f ) $\displaystyle \mathcal {H}$ (f )	(3.40)
	=	$\displaystyle {\frac{{A_{c}}}{{2}}}$ [ $\displaystyle \mathcal {M}$ (f - f_c) + $\displaystyle \mathcal {M}$ (f + f_c)] $\displaystyle \mathcal {H}$ (f )	(3.41)

Pour déterminer l'allure du filtre, il faut assurer que la démodulation soit en mesure de reconstituer le signal de départ. Considérons la détection cohérente qui consiste en la multiplication par la porteuse A_c'cos(2 $\pi$ f_ct).

v(t) = A_c'cos(2 $\displaystyle \pi$ f_ct)s(t)

(3.42)

$\displaystyle \mathcal {V}$ (f )= $\displaystyle {\frac{{A_{c}'}}{{2}}}$ [ $\displaystyle \mathcal {S}$ (f - f_c) + $\displaystyle \mathcal {S}$ (f + f_c)]

(3.43)

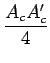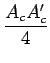$\displaystyle \mathcal {V}$ (f )	=	$\displaystyle {\frac{{A_{c}A_{c}'}}{{4}}}$ $\displaystyle \mathcal {M}$ (f )[ $\displaystyle \mathcal {H}$ (f - f_c) + $\displaystyle \mathcal {H}$ (f + f_c)]
	+	$\displaystyle {\frac{{A_{c}A_{c}'}}{{4}}}$ [ $\displaystyle \mathcal {M}$ (f - 2f_c) $\displaystyle \mathcal {H}$ (f - f_c) + $\displaystyle \mathcal {M}$ (f + 2f_c) $\displaystyle \mathcal {H}$ (f + f_c)]	(3.44)

Le second terme est éliminé à la réception par simple filtrage. Il reste alors un signal en bande de base n'ayant subi aucune distorsion à la condition que, $\forall$ f,

$\displaystyle \mathcal {H}$ (f - f_c) + $\displaystyle \mathcal {H}$ (f + f_c) = 1

(3.45)

Autrement dit, le filtre est symétrique en amplitude autour de la fréquence f_c; par ailleurs $\mathcal {H}$ (f_c) = 1/2. Le filtre idéal le plus simple est le filtre passe-haut ou passe-bas parfait, au droit de f_c, mais l'expression 3.45 permet d'autres choix de filtres, conduisant à la modulation à bande latérale résiduelle.

3.2.10.2 Démodulation

Le schéma de démodulation cohérente s'applique également au cas d'un signal à bande latérale unique; il est représenté à la figure 3.15.

**Figure 3.15:** Schéma de démodulation SSB.