Table des matières of 3.3.1 Principes et définitions

3.3.1 Principes et définitions

Dans la modulation angulaire, le signal modulé prend la forme

s(t) = A_ccos $\displaystyle \phi_{{i}}^{}$ (t)

(3.46)

où $\phi_{{i}}^{}$ (t), appelée phase instantanée du signal modulé, est une fonction du signal modulant. En l'absence de modulation, on aurait évidemment $\phi_{{i}}^{}$ (t) = 2 $\pi$ f_ct + $\phi_{{c}}^{}$ où $\phi_{{c}}^{}$ est la phase au temps t = 0. Remarquons que la modulation angulaire n'affecte pas l'amplitude la porteuse.

Définition 14 La déviation instantanée de phase est la grandeur définie par

$\displaystyle \triangle$ $\displaystyle \phi_{{i}}^{}$ (t) = $\displaystyle \phi_{{i}}^{}$ (t) - (2 $\displaystyle \pi$ f_ct + $\displaystyle \phi_{{c}}^{}$ )

(3.47)

Définition 15 L'amplitude de la déviation instantanée de phase

$\displaystyle \beta$ = max| $\displaystyle \triangle$ $\displaystyle \phi_{{i}}^{}$ (t)|

(3.48)

est appelée indice de modulation .

Elle joue un rôle important, comme nous le verrons ultérieurement. La déviation instantanée de phase peut être interprétée comme une variation de la fréquence.

Définition 16 Par définition, la quantité

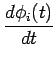f_i(t) = $\displaystyle {\frac{{1}}{{2\pi}}}$ $\displaystyle {\frac{{d\phi_{i}(t)}}{{dt}}}$

(3.49)

est la fréquence instantanée.

Bien entendu, en l'absence de modulation angulaire, on retrouve la fréquence de la porteuse f_c. Ce n'est pas tant la fréquence qui importe mais la différence entre la fréquence instantanée et la fréquence porteuse. Tout comme pour la phase, on définit la déviation instantanée de fréquence.

Définition 17 La déviation instantanée de fréquence $\triangle$ f_i(t) est l'écart entre la fréquence de la porteuse et la fréquence instantanée

$\displaystyle \triangle$ f_i(t) = f_i(t) - f_c

(3.50)

Définition 18 Le maximum de la déviation instantanée de fréquence $\triangle$ f_i(t) fournit l'excursion de fréquence $\triangle$ f définie par

$\displaystyle \triangle$ f = max| $\displaystyle \triangle$ f_i(t)|

(3.51)

Des définitions précises des divers types de modulation angulaire seront données plus loin. On peut déjà dire que la modulation angulaire consiste à faire varier, selon une loi linéaire bien précise, une des quantités $\triangle$ $\phi_{{i}}^{}$ (t) ou $\triangle$ f_i(t). Comme suite des définitions qui précèdent, il apparaît que l'on ne peut faire varier l'une sans l'autre; une modulation de phase entraîne donc une modulation de fréquence et inversement.

Dans le jargon technique, on utilise aussi le terme de taux de modulation : il s'agit de la quantité $\triangle$ f / $\triangle$ f_max, où $\triangle$ f_max est la valeur maximale de l'excursion de fréquence autorisée par les règlements régissant le partage des fréquences, par exemple par le Règlement des radiocommunications. Ainsi, en radiodiffusion sonore à modulation de fréquence, on impose $\triangle$ f_max = 75 [kHz].

À condition de faire varier un paramètre de la phase comme une fonction linéaire du signal modulant, on obtient une modulation appelée modulation angulaire. Dans cette modulation, le signal modulant m(t) est généralement un signal alternatif, tel qu'un signal sonore, oscillant entre -1 et +1. Pour l'instant, il s'agira d'un signal continu, auquel cas on parle de modulation angulaire analogique de type F3.

Parmi toutes les possibilités de modulation angulaire, on distingue la modulation de phase pure et la modulation de fréquence pure.

3.3.1.1 Modulation de phase pure

Définition 19 La modulation de phase (Phase Modulation, PM) consiste à faire varier la phase $\phi_{{i}}^{}$ (t) en fonction du signal modulant^3.3 m(t), à savoir (on prend $\phi_{{c}}^{}$ = 0)

$\displaystyle \phi_{{i}}^{}$ (t) = 2 $\displaystyle \pi$ f_ct + k_pm(t)

(3.52)

Le terme 2 $\pi$ f_ct représente la phase de la porteuse en l'absence de modulation. La présence d'une tension modulante affecte cette phase en fonction d'un coefficient k_p qui représente la sensibilité du modulateur; elle s'exprime en radians par volt. Le signal modulé vaut donc

s(t) = A_ccos(2 $\displaystyle \pi$ f_ct + k_pm(t))

(3.53)

La fréquence instantanée de la cosinusoïde est la dérivée de la phase divisée par 2 $\pi$

f_i(t) = $\displaystyle {\frac{{1}}{{2\pi}}}$ $\displaystyle {\frac{{d\phi_{i}(t)}}{{dt}}}$ = f_c + $\displaystyle {\frac{{k_{p}}}{{2\pi}}}$ $\displaystyle {\frac{{dm(t)}}{{dt}}}$

(3.54)

Il s'ensuit que la modulation de phase revient à modifier la fréquence de la porteuse. La déviation de fréquence instantanée vaut

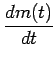$\displaystyle \triangle$ f_i(t) = $\displaystyle {\frac{{k_{p}}}{{2\pi}}}$ $\displaystyle {\frac{{dm(t)}}{{dt}}}$

(3.55)

3.3.1.2 Modulation de fréquence pure

Définition 20 Par définition de la modulation de fréquence (Frequency Modulation, FM), la déviation instantanée f_i(t) est proportionnelle au signal modulant

f_i(t) = f_c + k_fm(t)

(3.56)

La fréquence résultante est donc liée, via la sensibilité du modulateur k_f exprimée en [Hz/V], au signal modulant. La phase du signal modulé se calcule par l'intégrale de la fréquence instantanée (on prend $\phi_{{c}}^{}$ = 0)

$\displaystyle \phi_{{i}}^{}$ (t) = 2 $\displaystyle \pi$ f_ct + 2 $\displaystyle \pi$ k_f $\displaystyle \int_{{0}}^{{t}}$ m(t')dt'

(3.57)

Dès lors le signal modulé vaut

s(t) = A_ccos(2 $\displaystyle \pi$ f_ct + 2 $\displaystyle \pi$ k_f $\displaystyle \int_{{0}}^{{t}}$ m(t')dt')

(3.58)

Les relations 3.54 et 3.57 mettent bien en évidence qu'une modulation de phase entraîne une modulation de fréquence, et vice versa. Plus précisément, on peut affirmer que la modulation de phase se réduit à une modulation de fréquence par le signal modulant préalablement dérivé. Inversement, une modulation de fréquence est une modulation de phase par l'intégrale du signal modulant. Ces schémas sont représentés à la figure 3.16.

**Figure 3.16:** Liens entre modulation de phase et modulation de fréquence.

3.3.1.3 Notion de préaccentuation

Les opérations d'intégrale et de dérivée établissent un lien entre deux types de modulation angulaire. Plus généralement, la modulation angulaire regroupe tous les cas où $\triangle$ $\phi_{{i}}^{}$ (t) et $\triangle$ f_i(t) sont des fonctions linéaires du temps. Pour la commodité, on parle de modulation de fréquence avec préaccentuation; ce vocable désigne une modulation de fréquence pure par un signal obtenu par passage du signal modulant proprement dit m(t) au travers d'un système linéaire appelé filtre de préaccentuation. Si l'on note $\mathcal {H}$ (f ) la transmittance de ce filtre, l'ensemble de la chaîne de transmission peut être vu comme une paire constituée d'un modulateur et d'un démodulateur insérée entre un filtre de préaccentuation et un filtre de désaccentuation de transmittance 1/ $\mathcal {H}$ (f ).

La préaccentuation présente deux avantages: une meilleure résistance au bruit et une réalisation systématique à l'aide d'un modulateur en fréquence, techniquement plus aisée qu'une modulation de phase.

3.3.1.4 Illustration des techniques de modulation

En conséquence de la modulation de la phase, les passages par 0 de la fonction ne sont plus équidistants; par contre, l'enveloppe reste constante. La figure 3.17 montre un signal modulant original et les signaux modulés respectivement en amplitude, en phase et en fréquence.

**Figure 3.17:** Signal modulant et signaux modulés respectivement en AM, PM et FM.

Notes

... modulant ^3.3: Nous n'exigeons pas $\left\vert\vphantom{m(t)}\right.$ m(t) $\left.\vphantom{m(t)}\right\vert$ $\leq$ 1 en modulation angulaire.